【题目】如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号) 
参考答案:
【答案】解:∵△ABD是等边三角形,
∴∠B=60°,
∵∠BAC=90°,
∴∠C=180°﹣90°﹣60°=30°,
∵AB=2,
∴BC=2AB=4,
在Rt△ABC中,由勾股定理得:AC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴△ABC的周长是AC+BC+AB=2 ![]() +4+2=6+2
+4+2=6+2 ![]() .
.
答:△ABC的周长是6+2 ![]() .
.
【解析】根据等边三角形性质求出∠B=60°,求出∠C=30°,求出BC=4,根据勾股定理求出AC,相加即可求出答案.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和等边三角形的性质的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(x2)3=x6B.a3a2=a6C.(ab2)2=ab4D.(x3)2=x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、 是
是 的直径,
的直径, 是
是 的弦,且
的弦,且 ,过点
,过点 的切线与
的切线与 的延长线交于点
的延长线交于点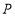 ,连接
,连接 .
.(1)求证:
 平分
平分 ;
;(2)求证:
 ;
;(3)若
 ,求
,求 的半径.
的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图12,已知抛物线
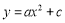 过点
过点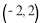 ,
,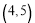 ,过定点
,过定点 的直线
的直线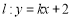 与抛物线交于
与抛物线交于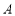 ,
,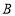 两点,点
两点,点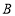 在点
在点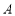 的右侧,过点
的右侧,过点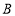 作
作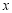 轴的垂线,垂足为
轴的垂线,垂足为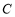 .
.(1)求抛物线的解析式;
(2)当点
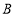 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段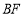 与
与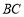 的数量关系(
的数量关系(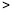 、
、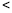 、
、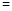 ),并证明你的判断;
),并证明你的判断;(3)
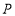 为
为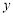 轴上一点,以
轴上一点,以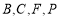 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点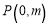 ,求自然数
,求自然数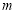 的值;
的值;(4)若
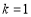 ,在直线
,在直线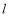 下方的抛物线上是否存在点
下方的抛物线上是否存在点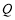 ,使得
,使得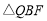 的面积最大,若存在,求出点
的面积最大,若存在,求出点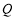 的坐标及
的坐标及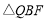 的最大面积,若不存在,请说明理由.
的最大面积,若不存在,请说明理由. 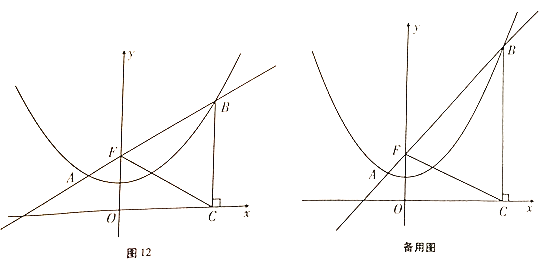
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC.
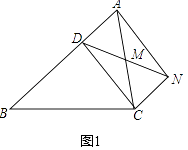
(1)求证:四边形ADCN是平行四边形.
(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外)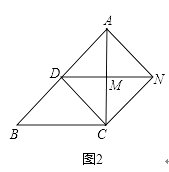
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的两个平方根分别是a+3和2﹣2a,则这个正数的立方根是_____.
相关试题

