【题目】已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC. 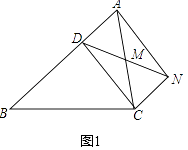
(1)求证:四边形ADCN是平行四边形.
(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外) 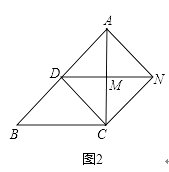
参考答案:
【答案】
(1)证明:∵CN∥AB,
∴∠DAM=∠NCM,
在△ADM和△CNM中,
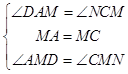 ,
,
∴△AMD≌△CMN(ASA),
∴MD=MN,
∴四边形ADCN是平行四边形
(2)解:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MC=MD,
∴AC=DN,
∴ADCN是矩形,
∵AC=BC,
∴AD=BD,
∵∠ACB=90°,
∴CD=AD=BD= ![]() AB,
AB,
∴ADCN是正方形,
∴AN=AD=BD=CD=CN.
【解析】(1)由CN∥AB,MA=MC,易证得△AMD≌△CMN,则可得MD=MN,即可证得:四边形ADCN是平行四边形.(2)由∠AMD=2∠MCD,可证得四边形ADCN是矩形,又由∠ACB=90°,AC=BC,可得四边形ADCN是正方形,继而求得答案.
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图12,已知抛物线
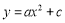 过点
过点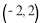 ,
,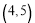 ,过定点
,过定点 的直线
的直线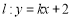 与抛物线交于
与抛物线交于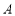 ,
,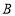 两点,点
两点,点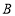 在点
在点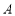 的右侧,过点
的右侧,过点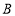 作
作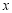 轴的垂线,垂足为
轴的垂线,垂足为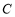 .
.(1)求抛物线的解析式;
(2)当点
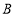 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段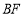 与
与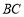 的数量关系(
的数量关系(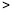 、
、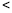 、
、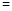 ),并证明你的判断;
),并证明你的判断;(3)
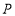 为
为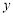 轴上一点,以
轴上一点,以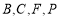 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点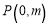 ,求自然数
,求自然数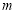 的值;
的值;(4)若
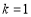 ,在直线
,在直线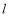 下方的抛物线上是否存在点
下方的抛物线上是否存在点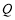 ,使得
,使得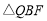 的面积最大,若存在,求出点
的面积最大,若存在,求出点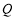 的坐标及
的坐标及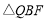 的最大面积,若不存在,请说明理由.
的最大面积,若不存在,请说明理由. 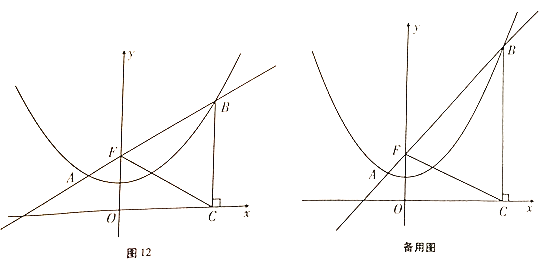
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的两个平方根分别是a+3和2﹣2a,则这个正数的立方根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,其中是中心对称图形有_____个.
①圆;②平行四边形;③长方形;④等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=5,an=3,则am+n=_____________.
相关试题

