【题目】如图,![]() 、
、![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,且
的弦,且![]() ,过点
,过点![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的半径.
的半径.

参考答案:
【答案】(1)详见解析;(2)详见解析;(3)5.
【解析】试题分析:(1)由BE∥CD知∠1=∠3,根据∠2=∠3即可得∠1=∠2;(2)连接EC、AC,由PC是⊙O的切线且BE∥DC,得∠1+∠4=90°,由∠A+∠2=90°且∠A=∠5知∠5+∠2=90°,根据∠1=∠2得∠4=∠5,从而证得△PBC∽△PCE,即可得结论;(3)由PC2=PBPE、BE﹣BP=PC=4求得BP=2、BE=6,作EF⊥CD可得PC=FE=4、FC=PE=8,再Rt△DEF≌Rt△BCP得DF=BP=2,据此得出CD的长即可.
试题解析:
(1)∵BE∥CD,
∴∠1=∠3,
又∵OB=OC,
∴∠2=∠3,
∴∠1=∠2,即BC平分∠ABP;
(2)如图,连接EC、AC,
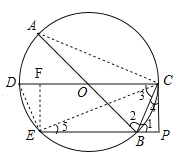
∵PC是⊙O的切线,
∴∠PCD=90°,
又∵BE∥DC,
∴∠P=90°,
∴∠1+∠4=90°,
∵AB为⊙O直径,
∴∠A+∠2=90°,
又∠A=∠5,
∴∠5+∠2=90°,
∵∠1=∠2,
∴∠5=∠4,
∵∠P=∠P,
∴△PBC∽△PCE,
∴![]() ,即PC2=PBPE;
,即PC2=PBPE;
(3)∵BE﹣BP=PC=4,
∴BE=4+BP,
∵PC2=PBPE=PB(PB+BE),
∴42=PB(PB+4+PB),即PB2+2PB﹣8=0,
解得:PB=2,
则BE=4+PB=6,
∴PE=PB+BE=8,
作EF⊥CD于点F,
∵∠P=∠PCF=90°,
∴四边形PCFE为矩形,
∴PC=FE=4,FC=PE=8,∠EFD=∠P=90°,
∵BE∥CD,
∴![]() ,
,
∴DE=BC,
在Rt△DEF和Rt△BCP中,
∵![]() ,
,
∴Rt△DEF≌Rt△BCP(HL),
∴DF=BP=2,
则CD=DF+CF=10,
∴⊙O的半径为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为6cm,则平行四边形ABCD的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是900°,这个多边形的边数是( )
A. 10 B. 9 C. 8 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(x2)3=x6B.a3a2=a6C.(ab2)2=ab4D.(x3)2=x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图12,已知抛物线
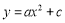 过点
过点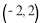 ,
,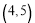 ,过定点
,过定点 的直线
的直线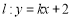 与抛物线交于
与抛物线交于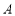 ,
,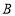 两点,点
两点,点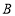 在点
在点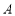 的右侧,过点
的右侧,过点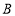 作
作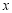 轴的垂线,垂足为
轴的垂线,垂足为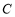 .
.(1)求抛物线的解析式;
(2)当点
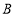 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段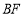 与
与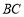 的数量关系(
的数量关系(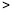 、
、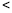 、
、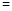 ),并证明你的判断;
),并证明你的判断;(3)
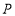 为
为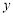 轴上一点,以
轴上一点,以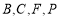 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点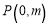 ,求自然数
,求自然数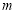 的值;
的值;(4)若
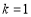 ,在直线
,在直线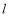 下方的抛物线上是否存在点
下方的抛物线上是否存在点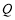 ,使得
,使得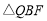 的面积最大,若存在,求出点
的面积最大,若存在,求出点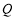 的坐标及
的坐标及 的最大面积,若不存在,请说明理由.
的最大面积,若不存在,请说明理由. 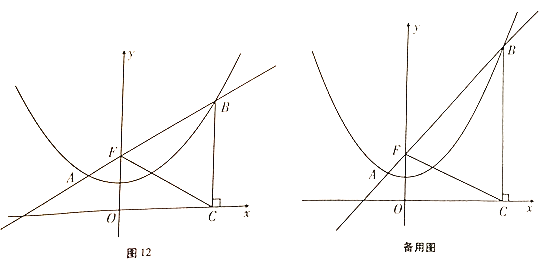
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
相关试题

