【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ![]() ;
;
其中正确的是(把你认为正确结论的序号都填上).
参考答案:
【答案】①②③
【解析】解:在Rt△ABC中,∵BC=2,∠BAC=30°,
∴AB=4,AC= ![]() =2
=2 ![]() ,①若C、O两点关于AB对称,如图1,
,①若C、O两点关于AB对称,如图1,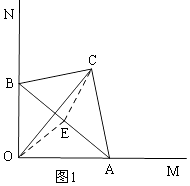
∴AB是OC的垂直平分线,
则OA=AC=2 ![]() ;
;
所以①正确;②如图1,取AB的中点为E,连接OE、CE,
∵∠AOB=∠ACB=90°,
∴OE=CE= ![]() AB=2,
AB=2,
当OC经过点E时,OC最大,
则C、O两点距离的最大值为4;
所以②正确;③如图2,同理取AB的中点E,则OE=CE,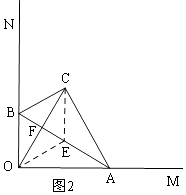
∵AB平分CO,
∴OF=CF,
∴AB⊥OC,
所以③正确;④如图3,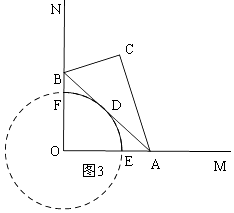
斜边AB的中点D运动路径是:以O为圆心,以2为半径的圆周的 ![]() ,
,
则: ![]() =π.
=π.
所以④不正确;
综上所述,本题正确的有:①②③;
所以答案是:①②③.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段,能构成三角形的是( )
A. 1,2,6 B. 1,2,3 C. 2,3,4 D. 2,2,4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是3cm和7cm,则它的周长为( )
A. 17cm B. 15cm C. 13cm D. 13cm或17cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】请用下表中的数据填空:
x
25
25.1
25.2
25.3
25.4
25.5
25.6
25.7
25.8
25.9
26
x2
625
630.01
635.04
640.09
645.16
650.25
655.36
660.49
665.64
670.81
676
(1)655.36的平方根是 .
(2)
 = .
= .(3) <
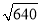 < .
< . -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)
阅读材料:
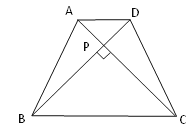
如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.
求证:S四边形ABCD=
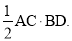
证明:AC⊥BD→
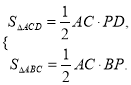
∴S四边形ABCD=S△ACD+S△ACB=
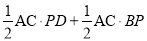
=
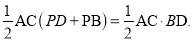
解答问题:
(1)上述证明得到的性质可叙述为_______________________________________.
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a2﹣2ab=﹣10,b2﹣2ab=16,那么﹣a2+4ab﹣b2的值是( )
A.6
B.-6
C.22
D.-22 -
科目: 来源: 题型:
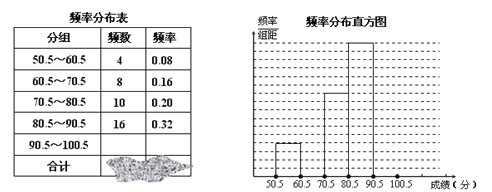
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答: 。
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答: 。
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答: 。
相关试题

