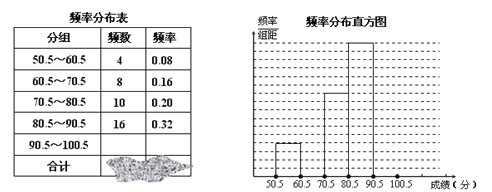
【题目】为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答: 。
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答: 。
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答: 。
参考答案:
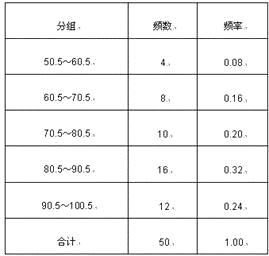
【答案】(1)
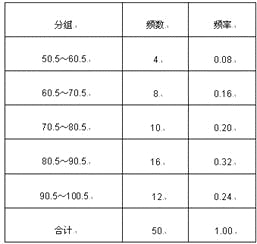
(2)如图:
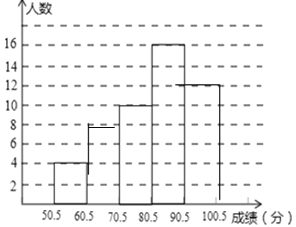
(3)80.5~90.5之间人数最多;
(4)216人.
【解析】试题分析:根据频数:总数=频率,各组频率之和为1,可解答表中数据,然后根据图表回答问题.
(1)各组频率之和为1,可知依次为右方是0.24,1.00,根据比例关系,可计算出左侧是8,12;
(2)如图:

(3)80.5~90.5之间人数最多;
(4)900×0.24=216,
答:该校成绩优秀的约为216人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ;
;
其中正确的是(把你认为正确结论的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)
阅读材料:
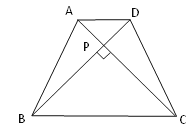
如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.
求证:S四边形ABCD=
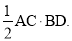
证明:AC⊥BD→
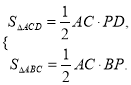
∴S四边形ABCD=S△ACD+S△ACB=
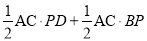
=
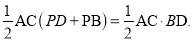
解答问题:
(1)上述证明得到的性质可叙述为_______________________________________.
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a2﹣2ab=﹣10,b2﹣2ab=16,那么﹣a2+4ab﹣b2的值是( )
A.6
B.-6
C.22
D.-22 -
科目: 来源: 题型:
查看答案和解析>>【题目】人体中成熟的红细胞的平均直径为0.000077厘米,用科学记数法表示为___________厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家承包了40亩大棚蔬菜,分别种植甲、乙两种蔬菜,有关成本,销售额如下表:
每亩成本
 万元
万元
每亩销售额
 万元
万元
甲

4
乙
3
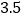
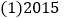 年,小明家种植甲蔬菜30亩,乙蔬菜10亩,求小明家这一年收益多少万元?
年,小明家种植甲蔬菜30亩,乙蔬菜10亩,求小明家这一年收益多少万元?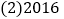 年,小明家继续用这40亩全部种植甲乙两种蔬菜,计划投入成本不少于141万元,若每亩种植成本、销售额和2015年一样,要获得最大收益,他家应该种植甲乙两种蔬菜各多少亩?
年,小明家继续用这40亩全部种植甲乙两种蔬菜,计划投入成本不少于141万元,若每亩种植成本、销售额和2015年一样,要获得最大收益,他家应该种植甲乙两种蔬菜各多少亩? 已知甲种蔬菜每亩需要有机肥600千克,乙种蔬菜每亩需要有机肥800千克
已知甲种蔬菜每亩需要有机肥600千克,乙种蔬菜每亩需要有机肥800千克 根据
根据 中的种植亩数,为节约运输成本,实际使用的运输每次装载的总量是计划的每次装载的总量的4倍,结果运输种植所需全部有机肥比原计划减少3次,求小明家原定的运输车辆每次可装载有机肥多少千克?
中的种植亩数,为节约运输成本,实际使用的运输每次装载的总量是计划的每次装载的总量的4倍,结果运输种植所需全部有机肥比原计划减少3次,求小明家原定的运输车辆每次可装载有机肥多少千克? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a﹣1)x>a﹣1的解集是x<1,则a的取值范围是( )
A. a>1 B. a>2 C. a<1 D. a<2
相关试题

