【题目】如图,正方形ABCD中,点E为边BC的上一动点,作AF⊥DE交DE、DC分别于P、F点,连PC
(1)若点E为BC的中点,求证:F点为DC的中点;
(2)若点E为BC的中点,PE=6,PC=![]() ,求PF的长.
,求PF的长.

参考答案:
【答案】(1)证明见解析;(2)2
【解析】
(1)先证得△ADF≌△DCE,推出DF=CE,由EC=![]() BC,BC=DC,继而可得DF=
BC,BC=DC,继而可得DF=![]() DC,即可求证结论;
DC,即可求证结论;
(2)延长PE到N,使得EN=PF,连接CN,易证△CEN≌△CFP,继而推出△NCP是等腰直角三角形,推出PN=PE+NE=PE+PF=![]() ,即可求解.
,即可求解.
证明:(1)∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,
∵AF⊥DE,
∴∠APD=∠DPF=90°,
∴∠ADP+∠DAF=90°,∠ADP+∠EDC=90°,
∴∠DAF=∠EDC,
在△ADF和△DCE中,
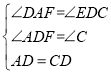 ,
,
∴△ADF≌△DCE(AAS),
∴DF=CE,
∵EC=![]() BC,BC=DC,
BC,BC=DC,
∴DF=![]() DC,
DC,
∴F点为DC的中点;
(2)延长PE到N,使得EN=PF,连接CN,
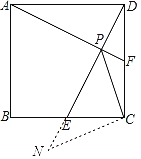
∵∠AFD=∠DEC,
∴∠CEN=∠CFP,
又∵E,F分别是BC,DC的中点,
∴CE=CF,
∵在△CEN和△CFP中
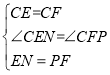 ,
,
∴△CEN≌△CFP(SAS),
∴CN=CP,∠ECN=∠PCF,
∵∠PCF+∠BCP=90°,
∴∠ECN+∠BCP=∠NCP=90°,
∴△NCP是等腰直角三角形,
∴PN=PE+NE=PE+PF=![]() ,
,
∴PF=![]() ﹣PE=8﹣6=2.
﹣PE=8﹣6=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF= ,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
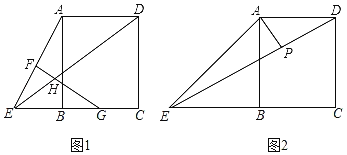
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求
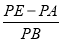 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60
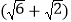 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120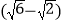 海里。
海里。
(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:
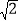 =1.41,
=1.41,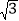 =1.73,
=1.73,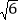 =2.45)
=2.45) -
科目: 来源: 题型:
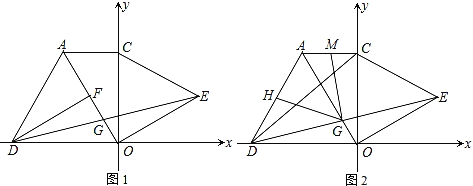
查看答案和解析>>【题目】如图,在平面直角坐标系中,∠ACO=90°,∠AOC=30°,分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE,DF⊥AO于F,连DE交AO于G.
(1)求证:△DFG≌△EOG;
(2)H为AD的中点,连HG,求证:CD=2HG;
(3)在(2)的条件下,AC=4,若M为AC的中点,求MG的长.
相关试题

