【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
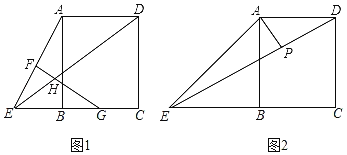
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求![]() 的值;
的值;
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
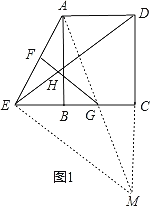
(1)连接AG,并延长AG交DC的延长线于M,连接EM,证明先证明△ABG≌△MCG(ASA),得到GA=GM,加上已知F为AE的中点,进而证明FG是△AEM的中位线,根据中位线的性质可得∠HGE=∠MEC,接下来用SAS证明△DEC≌△MEC,可得∠DEC=∠MEC,所以∠HEG=∠HGE,HE=HG即得以证明;
(2)过点B作BQ⊥BP交DE于Q,在△ABP和△EBQ中,根据三角形内角和定理及对顶角相等的性质,易得∠BEQ=∠BAP,由∠QBP=∠ABE=90°可得∠QBP=∠ABE=90°,又因为BE=AB,所以满足ASA,△BEQ≌△BAP可证;再根据全等三角形的性质可得BQ=BP,PA=QE,可证△PBQ是等腰直角三角形,![]() ,而PQ=
,而PQ=![]() PB,等量代换代入所求比例式,即可求解.
PB,等量代换代入所求比例式,即可求解.
(1)证明:连接AG,并延长AG交DC的延长线于M,连接EM,
 ,
,
∵G为BC的中点,
∴BG=CG,
∵四边形ABCD是矩形,
∴∠ABG=∠DCB=90°,
∴∠ABG=∠MCG=90°,
在△ABG和△MCG中,
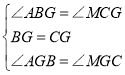 ,
,
∴△ABG≌△MCG(ASA),
∴GA=GM,
∵F为AE的中点,
∴FA=FE,
∴FG是△AEM的中位线,
∴FG∥EM,
∴∠HGE=∠MEC,
在△DCE和△MCE中,
![]()
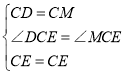 ,
,
∴△DEC≌△MEC(SAS),
∴∠DEC=∠MEC,
∵∠HGE=∠MEC,
∴∠HEG=∠HGE,
∴HE=HG;
(2)过点B作BQ⊥BP交DE于Q,则∠QBP=90°,
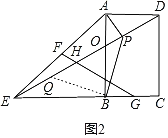
∵AP⊥DE,四边形ABCD是矩形,
∴∠APE=∠ABE=90°,
∵∠APO+∠AOP+∠BAP=180°,∠EOB+∠ABE+∠BEP=180°,∠AOP=∠EOB,
∴∠BEQ=∠BAP,
∵∠QBP=∠ABE=90°,
∴∠EBQ=∠ABP=90°﹣∠ABQ,
在△ABP和△EBQ中,
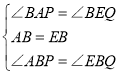 ,
,
∴△BEQ≌△BAP(ASA),
∴BQ=BP,PA=QE,
∴△PBQ是等腰直角三角形,
∴PQ=![]() PB,
PB,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF= ,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E为边BC的上一动点,作AF⊥DE交DE、DC分别于P、F点,连PC
(1)若点E为BC的中点,求证:F点为DC的中点;
(2)若点E为BC的中点,PE=6,PC=
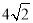 ,求PF的长.
,求PF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60
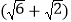 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120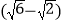 海里。
海里。
(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:
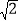 =1.41,
=1.41,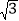 =1.73,
=1.73,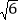 =2.45)
=2.45) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,∠ACO=90°,∠AOC=30°,分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE,DF⊥AO于F,连DE交AO于G.
(1)求证:△DFG≌△EOG;
(2)H为AD的中点,连HG,求证:CD=2HG;
(3)在(2)的条件下,AC=4,若M为AC的中点,求MG的长.
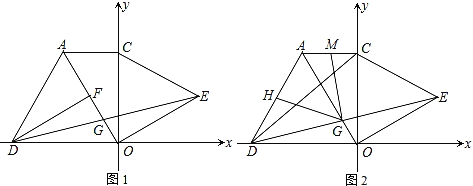
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填在相应的集合里:
-3.8,-10,4.3,-|-
 |,42,0,-(-
|,42,0,-(- ).0.275,
).0.275,整数集合:{ …};
分数集合:{ …};
正数集合:{ …};
负数集合:{ …};
相关试题

