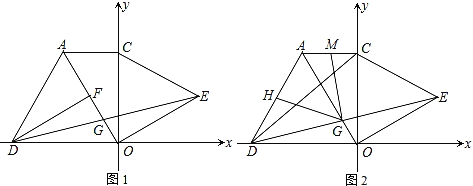
【题目】如图,在平面直角坐标系中,∠ACO=90°,∠AOC=30°,分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE,DF⊥AO于F,连DE交AO于G.
(1)求证:△DFG≌△EOG;
(2)H为AD的中点,连HG,求证:CD=2HG;
(3)在(2)的条件下,AC=4,若M为AC的中点,求MG的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)本题考查全等三角形的判定,通过等边三角形的性质利用AAS定理解答本题.
(2)本题考查三角形中位线定理以及全等三角形的判定,通过构造辅助线利用SAS定理解答.
(3)本题考查三角形中位线定理以及等边三角形的证明,通过构造辅助线,结合角度的计算加以证明,最后求解边长.
证明:(1)如图1,∵∠AOC=30°,
∴∠GOE=90°.
设AC=a,则OA=2a,OE=OC=![]() a,
a,
在等边△AOD中,DF⊥OA,
∴DF=![]() a,
a,
∴DF=OE.
又∵∠DGF=∠EGO,∠DFG=∠EOG,
∴△DFG≌△EOG(AAS).
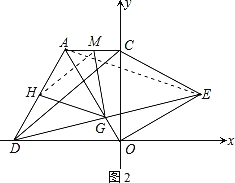
(2)如下图图2所示,连接AE,
∵H、G分别为AD、DE的中点,
∴HG∥AE,HG=![]() AE.
AE.
∵DO=AO,CO=OE,∠DOC=∠AOE=90°,
∴△DOC≌△AOE(SAS),
∴DC=AE,
∴DC=2HG.
(3)如下图图2所示,连接HM,
∵H、M分别为AD、AC的中点,
∴HM=![]() CD.
CD.
∵DC=2HG,
∴HM=HG.
又∠DHG=∠DAE=60°+∠OAE=60°+∠ODC,∠AHM=∠ADC,
∴∠MHG=180°﹣∠AHM﹣∠DHG=180°﹣∠ADC﹣60°﹣∠ODC=120°﹣(∠ADC+∠ODC)=120°﹣∠ADO=60°,
∴△HMG为等边三角形.
∵AC=4,
∴OA=OD=8,OC=![]() ,CD=
,CD=![]() ,
,
∴MG=HG=![]() CD=
CD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E为边BC的上一动点,作AF⊥DE交DE、DC分别于P、F点,连PC
(1)若点E为BC的中点,求证:F点为DC的中点;
(2)若点E为BC的中点,PE=6,PC=
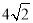 ,求PF的长.
,求PF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
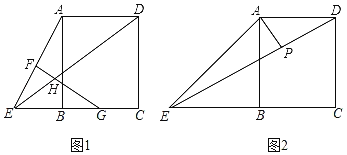
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求
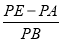 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60
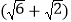 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120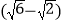 海里。
海里。
(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:
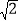 =1.41,
=1.41,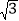 =1.73,
=1.73,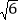 =2.45)
=2.45) -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填在相应的集合里:
-3.8,-10,4.3,-|-
 |,42,0,-(-
|,42,0,-(- ).0.275,
).0.275,整数集合:{ …};
分数集合:{ …};
正数集合:{ …};
负数集合:{ …};
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,且∠ABC=120°,E是BC的中点,P为BD上一点,且△PCE的周长最小,则△PCE的周长的最小值为( )
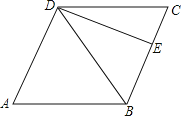
A.
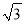 +1B.
+1B.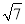 +1C.2
+1C.2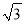 +1D.2
+1D.2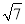 +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E为ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF,若∠BDC=81°,则∠C=_____.

相关试题

