【题目】如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标.

参考答案:
【答案】(1)m=3;(2)A点的坐标是(1,4),B点的坐标是(6,9).
【解析】试题分析:(1)根据抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,可得抛物线与x轴只有一个交点,所以△=0,据此求出m的值是多少即可.
(2)联立抛物线与一次函数的解析式,求出A、B两点的坐标各是多少即可.
试题解析:
(1)∵抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,
∴抛物线与x轴只有一个交点,
∴(m+3)2-4×9=0,
解得m=3或m=-9,
又∵-![]() >0,
>0,
∴m>-3,
∴m=3.
(2)由(1),可得m=3,
∴抛物线的解析式为:y=x2-6x+9,
联立![]() ,
,
解得![]() ,
,
根据图示,可得A点的横坐标小于B点的横坐标,
∴A点的坐标是(1,4),B两点的坐标是(6,9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求
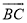 的长.
的长.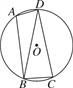
-
科目: 来源: 题型:
查看答案和解析>>【题目】网上销售已成为产品销售的一种重要方式,很多大学生也在网上开起了网店,某手机销售网店正在代理销售一种新型智能手机,手机每部进价为1000元,经过试销发现:售价x(元/部)与每天交易量y(部)之间满足如图所示关系。
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售价x之间的函数关系式.若你是网店老板,会将价格定为多少,使每天获得的利润最大,最大利润是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF= ,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E为边BC的上一动点,作AF⊥DE交DE、DC分别于P、F点,连PC
(1)若点E为BC的中点,求证:F点为DC的中点;
(2)若点E为BC的中点,PE=6,PC=
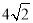 ,求PF的长.
,求PF的长.
相关试题

