【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
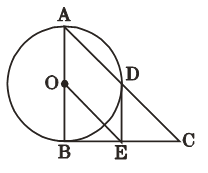
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:![]()
(3)若tanC=![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
参考答案:
【答案】(1)DE与⊙O相切,理由见解析; (2)证明见解析;(3)![]()
【解析】
解:(1) DE与⊙O相切
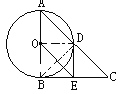
理由如下:连接OD,BD,
∵AB是直径,∴∠ADB=∠BDC=90°
∵E是BC的中点,∴DE=BE=CE,∴∠EDB=∠EBD,
∵OD=OB,∴∠OBD=∠ODB.
∴∠EDO=∠EBO=90°
∴DE与⊙O相切
(2)证明:由题意得OE是的△ABC的中位线,∴AC=2OE
∵∠ABC=∠BDC=900,∠C=∠C ,∴△ABC∽△BDC
∴![]() ,∴BC2=CD·AC,∴BC2=2CD·OE
,∴BC2=CD·AC,∴BC2=2CD·OE
(3) ∵DE=2 BC=4 AB=4. tanC![]()
tanA=![]() , 设BD=AD
, 设BD=AD![]() ,
,

![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级某班同学在“五四”游园活动中进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为A,B,C,随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2mx+m+2的图象与x轴交于A(﹣1,0),B两点,在x轴上方且平行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
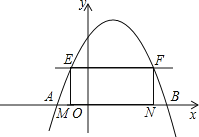
(1)求m的值及抛物线的顶点坐标;
(2)设BN=t,矩形EMNF的周长为C,求C与t的函数表达式;
(3)当矩形EMNF的周长为10时,将△ENM沿EN翻折,点M落在坐标平面内的点记为M',试判断点M'是否在抛物线上?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AC,BD是⊙O的两条直径,首位顺次连接A,B,C,D得到四边形ABCD,若AD=3,∠BAC=30°,则图中阴影部分的面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为
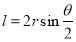 ,从而
,从而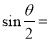
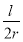 ,综合上述材料当
,综合上述材料当 时,
时,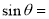 ______.
______.
相关试题

