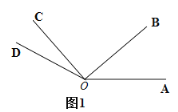
【题目】如图1,![]() ,
,![]() ,
,![]() ,把
,把![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转一周,同时
的速度逆时针方向旋转一周,同时![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,当
的速度逆时针方向旋转,当![]() 停止旋转时
停止旋转时![]() 也随之停止旋转.设旋转后的两个角分别记为
也随之停止旋转.设旋转后的两个角分别记为![]() 、
、![]() ,旋转时间为
,旋转时间为![]() 秒.
秒.
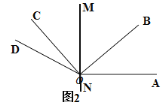
(1)如图2,直线![]() 垂直于
垂直于![]() ,将
,将![]() 沿直线
沿直线![]() 翻折至
翻折至![]() ,请你直接写出
,请你直接写出![]() 的度数,不必说明理由;
的度数,不必说明理由;
(2)如图1,在旋转过程中,若射线![]() 与
与![]() 重合时,求
重合时,求![]() 的值;
的值;
(3)如图1,在旋转过程中,当![]() 时,直接写出
时,直接写出![]() 的值,不必说明理由.
的值,不必说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)5秒或9秒
;(3)5秒或9秒
【解析】
(1)根据轴对称的性质求出∠MOD=MOD′=60°, 根据角的和差求出∠MOB,进而可求出BOD′的值;
(2)求出∠BOC=70°,然后根据射线![]() 与
与![]() 重合时,射线
重合时,射线![]() 比
比![]() 多走了70°列方程求解即可;
多走了70°列方程求解即可;
(3)分相遇前和相遇后两种情况列方程求解即可.
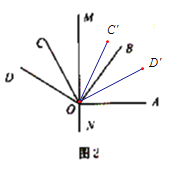
解:(1)如图2,
∵![]() ,
,![]() ,
,![]() ,
,
∴∠MOD=MOD′=150°-90°=60°, ∠MOB=90°-50°=40°,
∴BOD′=60°-40°=20°;
(2)∵![]() ,
,![]() ,
,![]() ,
,
∴∠BOC=70°.
由题意得
20t-10t=70,
∴t=7;
(3)①相遇前,由题意得
20t-10t=70-20,
∴t=5;
②相遇后,由题意得
20t-10t=70+20,
∴t=9;
综上可知,当![]() 时,
时,![]() 的值是5秒或9秒.
的值是5秒或9秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
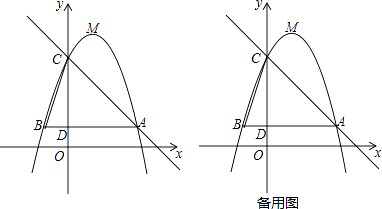
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:整式与分式
(1)(2x+1)(2x﹣1)﹣(x+1)(3x﹣2)
(2)( ﹣x+1)÷
﹣x+1)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED


若要使点F 恰好落在射线EB 上,求点P 运动的时间t
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
相关试题

