【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.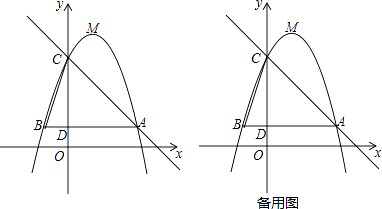
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
参考答案:
【答案】
(1)解:把点A(3,1),点C(0,4)代入二次函数y=﹣x2+bx+c得,
![]() 解得
解得 ![]()
∴二次函数解析式为y=﹣x2+2x+4,
配方得y=﹣(x﹣1)2+5,
∴点M的坐标为(1,5);
(2)解:设直线AC解析式为y=kx+b,把点A(3,1),C(0,4)代入得,
![]() 解得
解得 ![]()
∴直线AC的解析式为y=﹣x+4,如图所示,对称轴直线x=1与△ABC两边分别交于点E、点F
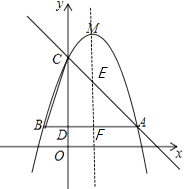
把x=1代入直线AC解析式y=﹣x+4解得y=3,则点E坐标为(1,3),点F坐标为(1,1)
∴1<5﹣m<3,解得2<m<4
(3)解:连接MC,作MG⊥y轴并延长交AC于点N,则点G坐标为(0,5)
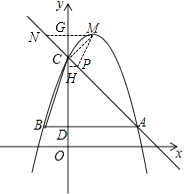
∵MG=1,GC=5﹣4=1
∴MC= ![]() =
= ![]() ,
,
把y=5代入y=﹣x+4解得x=﹣1,则点N坐标为(﹣1,5),
∵NG=GC,GM=GC,
∴∠NCG=∠GCM=45°,
∴∠NCM=90°,
由此可知,若点P在AC上,则∠MCP=90°,则点D与点C必为相似三角形对应点
①若有△PCM∽△BDC,则有 ![]()
∵BD=1,CD=3,
∴CP= ![]() =
= ![]() =
= ![]() ,
,
∵CD=DA=3,
∴∠DCA=45°,
若点P在y轴右侧,作PH⊥y轴,
∵∠PCH=45°,CP= ![]()
∴PH= ![]() =
= ![]()
把x= ![]() 代入y=﹣x+4,解得y=
代入y=﹣x+4,解得y= ![]() ,
,
∴P1( ![]() );
);
同理可得,若点P在y轴左侧,则把x=﹣ ![]() 代入y=﹣x+4,解得y=
代入y=﹣x+4,解得y= ![]()
∴P2( ![]() );
);
②若有△PCM∽△CDB,则有 ![]()
∴CP= ![]() =3
=3 ![]()
∴PH=3 ![]() ÷
÷ ![]() =3,
=3,
若点P在y轴右侧,把x=3代入y=﹣x+4,解得y=1;
若点P在y轴左侧,把x=﹣3代入y=﹣x+4,解得y=7
∴P3(3,1);P4(﹣3,7).
∴所有符合题意得点P坐标有4个,分别为P1( ![]() ),P2(
),P2( ![]() ),P3(3,1),P4(﹣3,7).
),P3(3,1),P4(﹣3,7).
【解析】(1)将点A、点C的坐标代入函数解析式,即可求出b、c的值,通过配方法得到点M的坐标;(2)点M是沿着对称轴直线x=1向下平移的,可先求出直线AC的解析式,将x=1代入求出点M在向下平移时与AC、AB相交时y的值,即可得到m的取值范围;(3)由题意分析可得∠MCP=90°,则若△PCM与△BCD相似,则要进行分类讨论,分成△PCM∽△BDC或△PCM∽△CDB两种,然后利用边的对应比值求出点坐标.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
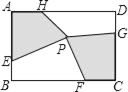
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2,则四边形PFCG的面积为_______cm2.
-
科目: 来源: 题型:
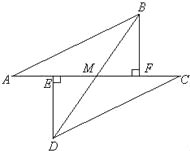
查看答案和解析>>【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
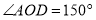 ,
,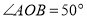 ,
,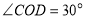 ,把
,把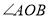 绕
绕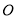 点以每秒
点以每秒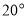 的速度逆时针方向旋转一周,同时
的速度逆时针方向旋转一周,同时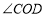 绕
绕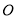 点以每秒
点以每秒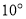 的速度逆时针方向旋转,当
的速度逆时针方向旋转,当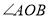 停止旋转时
停止旋转时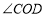 也随之停止旋转.设旋转后的两个角分别记为
也随之停止旋转.设旋转后的两个角分别记为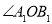 、
、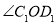 ,旋转时间为
,旋转时间为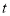 秒.
秒.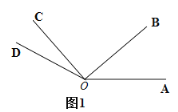
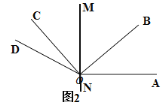
(1)如图2,直线
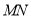 垂直于
垂直于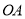 ,将
,将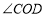 沿直线
沿直线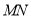 翻折至
翻折至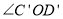 ,请你直接写出
,请你直接写出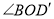 的度数,不必说明理由;
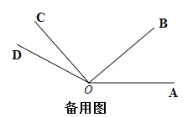
的度数,不必说明理由;(2)如图1,在旋转过程中,若射线
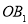 与
与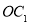 重合时,求
重合时,求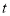 的值;
的值;(3)如图1,在旋转过程中,当
 时,直接写出
时,直接写出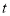 的值,不必说明理由.
的值,不必说明理由.
相关试题

