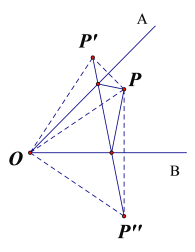
【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
参考答案:
【答案】C
【解析】
本题关键是根据轴对称,得到相等的角,进行相加得到直角,再得到三条线段P'O=PO= P'O,从而得到是等腰直角三角形.
解:如下图所示,连结P'O、PO、P'O,
∵P'与P关于OA对称
∴∠P'OA=∠POA ,P'O=PO
同理∠P'OB=∠POB ,P'O=PO
∠POA+∠POB=∠AOB=45°
∴∠P'OA+∠P'OB=∠POA+∠POB=45°
∴∠P'OA+∠P'OB+∠POA+∠POB=45°+45°=90°
∴△OP 'P'是直角三角形.
由P'O=PO和 P'O=PO得P'O= P'O
∴△OP'P'是等腰直角三角形.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
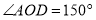 ,
,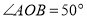 ,
,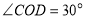 ,把
,把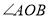 绕
绕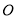 点以每秒
点以每秒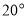 的速度逆时针方向旋转一周,同时
的速度逆时针方向旋转一周,同时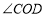 绕
绕 点以每秒
点以每秒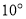 的速度逆时针方向旋转,当
的速度逆时针方向旋转,当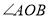 停止旋转时
停止旋转时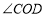 也随之停止旋转.设旋转后的两个角分别记为
也随之停止旋转.设旋转后的两个角分别记为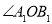 、
、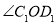 ,旋转时间为
,旋转时间为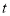 秒.
秒.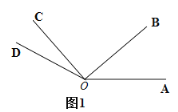
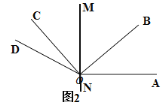
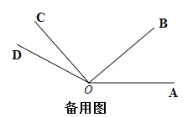
(1)如图2,直线
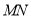 垂直于
垂直于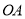 ,将
,将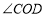 沿直线
沿直线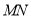 翻折至
翻折至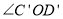 ,请你直接写出
,请你直接写出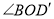 的度数,不必说明理由;
的度数,不必说明理由;(2)如图1,在旋转过程中,若射线
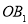 与
与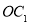 重合时,求
重合时,求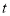 的值;
的值;(3)如图1,在旋转过程中,当
 时,直接写出
时,直接写出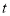 的值,不必说明理由.
的值,不必说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:整式与分式
(1)(2x+1)(2x﹣1)﹣(x+1)(3x﹣2)
(2)( ﹣x+1)÷
﹣x+1)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED


若要使点F 恰好落在射线EB 上,求点P 运动的时间t
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.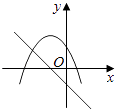
B.
C.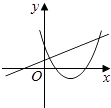
D.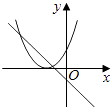
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.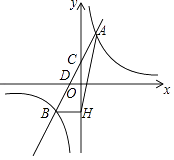
(1)求一次函数和反比例函数的解析式;
(2)求△ABH面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC 中,∠CAB=90°,AC=AB,点 D、E 是 BC 上的两点,且∠DAE=45°,△ADC 与△ADF 关于直线AD 对称.
(1)求证:△AEF≌△AEB;
(2)求∠DFE 的度数.
相关试题

