【题目】如图,在△ABC中,AB=17cm,AC=8cm,BC=15cm,将AC沿AE折叠,使得点C与AB上的点D重合.
(1)证明:△ABC是直角三角形;
(2)求△AEB的面积.

参考答案:
【答案】(1)证明见解析;(2)S△ABE=![]() .
.
【解析】
(1)根据勾股定理的逆定理即可判定△ABC是直角三角形;
(2)由翻折不变性可知:EC=DE,AC=AD=8cm,∠ADE=∠C=∠BDE=90°,设EC=DE=x,在Rt△BDE中,根据勾股定理列出方程,求出![]() 的值,根据三角形的面积公式进行求解即可.
的值,根据三角形的面积公式进行求解即可.
解:(1)∵AC2+BC2=82+152=289,AB2=289,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
(2)由翻折不变性可知:EC=DE,AC=AD=8cm,∠ADE=∠C=∠BDE=90°,
设EC=DE=x,在Rt△BDE中,∵DE2+BD2=BE2,
∴x2+92=(15-x)2,解得x=![]() .
.
∴DE=![]()
∴S△ABE=![]() ×AB×DE=
×AB×DE=![]() ×17
×17![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程的解法中,错误的个数是( )
①方程2x-1=x+1移项,得3x=0
②方程
 =1去分母,得x-1=3=x=4
=1去分母,得x-1=3=x=4③方程1-
 去分母,得4-x-2=2(x-1)
去分母,得4-x-2=2(x-1)④方程
 去分母,得2x-2+10-5x=1
去分母,得2x-2+10-5x=1A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】能够铺满地面的正多边形组合是( )
A. 正三角形和正五边形B. 正方形和正六边形
C. 正方形和正五边形D. 正五边形和正十边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形纸片
 折叠,使点
折叠,使点 落在边
落在边 上的
上的 处,点
处,点 落在
落在 处,若
处,若 ,则
,则 的度数为( )
的度数为( )
A. 100°B. 110°C. 120°D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角尺△ABC与△ADE的两条斜边在一条直线上,直尺的一边GF∥AC,则∠DFG的度数为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于
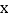 的方程
的方程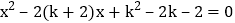 .
.(1)若这个方程有两个不相等的实数根,求
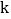 的取值范围;
的取值范围;(2)若此方程有一个根是1,求
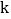 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为( )
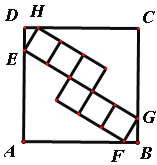
A.6 B.5 C.2
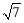 D.
D.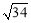
相关试题

