搜索
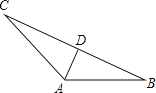
【题目】如图，在△ABC中，∠CAB=120°，AD是∠CAB的平分线，AC=10，AB=8．
（1）求
；（2）求AD的长．
参考答案：
【答案】（1）
；（2）
.
【解析】试题分析：(1)、过点C作CE∥AB，交AD的延长线于E，根据角平分线以及平行线的性质得出△ACE为等边三角形，根据平行得出△CDE∽△BDA，即
，从而得出答案；(2)、根据三角形相似得出
，从而求出AD的长度．
试题解析：解：（1）过点C作CE∥AB，交AD的延长线于E，
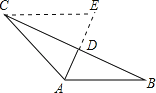
∵AD平分∠CAB，∠CAB=120°， ∴∠CAD=∠BAD=60°．
∵CE∥AB， ∴∠E=∠BAD=60°， ∴△ACE是等边三角形， ∴CE=AC=10．
又∵CE∥AB， ∴△CDE∽△BDA， ∴
=
=
（2）由（1）知，△ACE是等边三角形， ∴AE=10． ∵CE∥AB，
∴
∴AD=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的文字，解答问题：大家知道
是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，但是由于1＜＜2，所以的整数部分为1，将减去其整数部分1，差就是小数部分
，根据以上的内容，解答下面的问题：（1）
的整数部分是______，小数部分是______；（2）
的整数部分是______，小数部分是_____；（3）若设
整数部分是x，小数部分是y，求x﹣
y的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于一次函数
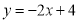，下列结论正确的是（ ）A.函数值随自变量的增大而增大
B.函数的图象不经过第一象限
C.函数的图象向下平移4个单位长度得
的图象D.函数的图象与
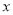轴的交点坐标是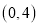
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P、Q分别是正方形ABCD的边AB、BC上的点，且BP＝BQ，过点B作PC的垂线，垂足为点H，连接HD、HQ. （14分）
(1)图中有________对相似三角形；
(2)若正方形ABCD的边长为1，P为AB的三等分点，求△BHQ的面积；
(3)求证：DH⊥HQ.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂为了扩大生产，决定购买8台机器用于生产零件，现有甲、乙两种机器可供选择，其中甲型机器每日生产零件100个，乙型机器每日生产零件60个，经调查，购买3台甲型机器和2台乙型机器共需要31万元，购买一台甲型机器比购买一台乙型机器多2万元．
(1)求甲、乙两种机器每台各多少万元？
(2)如果工厂买机器的预算资金不超过46万元，那么该工厂有哪几种购买方案？
(3)在(2)的条件下，如果要求该工厂购进的8台机器生产零件的日产量不低于550个，那么为了节约资金，应该选择哪种方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两班举行电脑汉字输入比赛，参赛学生每分输入汉字的个数统计结果如下表：
班级
参加人数
中位数
方差
平均数
甲
55
149
1.91
135
乙
55
151
1.10
135
某同学分析上表后得到如下结论：
①甲、乙两班学生平均成绩相同；
②乙班优秀的人数多于甲班优秀的人数（每分输入汉字个数
为优秀）③甲班成绩的波动比乙班大．
上述结论中正确的是（ ）
A.①②③B.①②C.①③D.②③
相关试题
