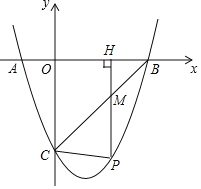
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
参考答案:
【答案】(1)二次函数的表达式y=x2﹣2x﹣3;(2)①PM最大=![]() ;②P(1,﹣4)或(
;②P(1,﹣4)或(![]() ,﹣2
,﹣2![]() ﹣1).
﹣1).
【解析】(1)根据待定系数法,可得答案;
(2)①根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
②根据等腰三角形的定义,可得方程,根据解方程,可得答案.
(1)将A,B,C代入函数解析式,
得 ,解得
,解得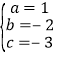 ,
,
这个二次函数的表达式y=x2﹣2x﹣3;
(2)设BC的解析式为y=kx+b,
将B,C的坐标代入函数解析式,得
![]() ,解得
,解得![]() ,
,
BC的解析式为y=x﹣3,
设M(n,n﹣3),P(n,n2﹣2n﹣3),
PM=(n﹣3)﹣(n2﹣2n﹣3)=﹣n2+3n=﹣(n﹣![]() )2+
)2+![]() ,
,
当n=![]() 时,PM最大=
时,PM最大=![]() ;
;
②当PM=PC时,(﹣n2+3n)2=n2+(n2﹣2n﹣3+3)2,
解得n1=0(不符合题意,舍),n2=2,
n2﹣2n﹣3=-3,
P(2,-3);
当PM=MC时,(﹣n2+3n)2=n2+(n﹣3+3)2,
解得n1=0(不符合题意,舍),n2=3+![]() (不符合题意,舍),n3=3-
(不符合题意,舍),n3=3-![]() ,
,
n2﹣2n﹣3=2-4![]() ,
,
P(3-![]() ,2-4
,2-4![]() );
);
综上所述:P(2,﹣3)或(3-![]() ,2﹣4
,2﹣4![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:
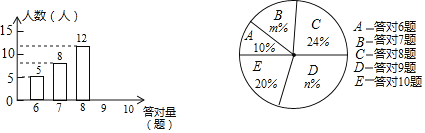
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=
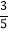 ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.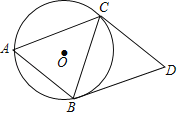
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:若要比较
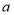 与
与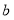 的大小.我们可以利用不等式的性质来说明:
的大小.我们可以利用不等式的性质来说明:例加:若
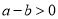 ,则
,则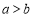 ;若
;若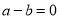 ,则
,则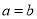 ;若
;若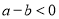 ,则
,则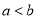 .
.像上述比较两个代数式大小的方法叫做作差法.
如:某同学需要比较
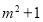 与
与 的大小,做法为
的大小,做法为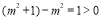 ,则
,则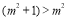 .试解答下列问题:
.试解答下列问题:(1) 比较大小:
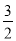
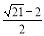
(2) 若
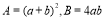 ,试用作差法比较
,试用作差法比较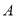 与
与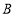 的大小关系,并说明理由;
的大小关系,并说明理由;(3)若某三角形的底和高均为
 ,某长方形的长宽为
,某长方形的长宽为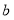 和
和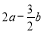 ,试比较这两个图形的面积大小,并说明理由;(其中
,试比较这两个图形的面积大小,并说明理由;(其中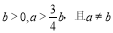 )
)(4)“无字证明”是数学中非常重要的一种解决方法.课本在证明
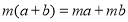 时,运用了如图中的图形面积来证明.某同学提出运用图形的几何意义的方法不仅可以解决等式的证明,也可以解决不等式的相关证明.如对(2)问中的
时,运用了如图中的图形面积来证明.某同学提出运用图形的几何意义的方法不仅可以解决等式的证明,也可以解决不等式的相关证明.如对(2)问中的 的大小关系的证明,当
的大小关系的证明,当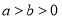 时,若使用图形的几何意义可以更为直观解决,请你画出符合题意的图形,并简要说明.
时,若使用图形的几何意义可以更为直观解决,请你画出符合题意的图形,并简要说明.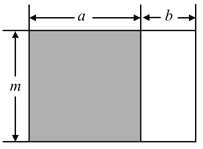
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:
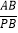 =
=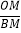 ;
;(3)若AO=2
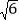 ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.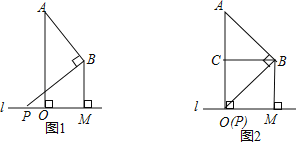
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,直线AB与
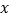 轴交于点A(-2,0),与
轴交于点A(-2,0),与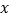 轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线
轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线 上,则
上,则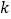 的值( )
的值( )
A. -4 B. -2 C.
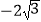 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,G是它的重心,AG⊥CD,如果
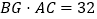 ,则△AGC的面积的最大值是( )
,则△AGC的面积的最大值是( )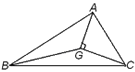
A.
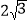 B. 8 C.
B. 8 C. 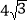 D. 6
D. 6
相关试题

