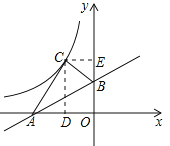
【题目】如图:在平面直角坐标系中,直线AB与![]() 轴交于点A(-2,0),与
轴交于点A(-2,0),与![]() 轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线
轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() 上,则
上,则![]() 的值( )
的值( )

A. -4 B. -2 C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,由折叠的性质易得∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,用锐角三角函数的定义得CD,CE,得点C的坐标,易得k.
设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴.
∵将△ABO沿直线AB翻折,∴∠CAB=∠OAB=30°,AC=AO=2,∠ACB=∠AOB=90°,∴CD=y=ACsin60°=2×![]() =
=![]() .
.
∵∠ACB=∠DCE=90°,∴∠BCE=∠ACD=30°.
∵BC=BO=AOtan30°=2×![]() =
=![]() ,CE=|x|=BCcos30°=
,CE=|x|=BCcos30°=![]() =1.
=1.
∵点C在第二象限,∴x=﹣1.
∵点C恰好落在双曲线y=![]() (k≠0)上,∴k=xy=﹣1×
(k≠0)上,∴k=xy=﹣1×![]() =﹣
=﹣![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:若要比较
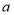 与
与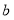 的大小.我们可以利用不等式的性质来说明:
的大小.我们可以利用不等式的性质来说明:例加:若
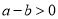 ,则
,则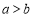 ;若
;若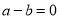 ,则
,则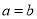 ;若
;若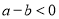 ,则
,则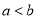 .
.像上述比较两个代数式大小的方法叫做作差法.
如:某同学需要比较
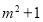 与
与 的大小,做法为
的大小,做法为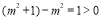 ,则
,则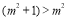 .试解答下列问题:
.试解答下列问题:(1) 比较大小:
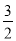
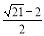
(2) 若
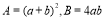 ,试用作差法比较
,试用作差法比较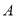 与
与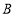 的大小关系,并说明理由;
的大小关系,并说明理由;(3)若某三角形的底和高均为
 ,某长方形的长宽为
,某长方形的长宽为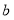 和
和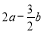 ,试比较这两个图形的面积大小,并说明理由;(其中
,试比较这两个图形的面积大小,并说明理由;(其中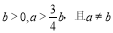 )
)(4)“无字证明”是数学中非常重要的一种解决方法.课本在证明
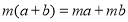 时,运用了如图中的图形面积来证明.某同学提出运用图形的几何意义的方法不仅可以解决等式的证明,也可以解决不等式的相关证明.如对(2)问中的
时,运用了如图中的图形面积来证明.某同学提出运用图形的几何意义的方法不仅可以解决等式的证明,也可以解决不等式的相关证明.如对(2)问中的 的大小关系的证明,当
的大小关系的证明,当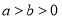 时,若使用图形的几何意义可以更为直观解决,请你画出符合题意的图形,并简要说明.
时,若使用图形的几何意义可以更为直观解决,请你画出符合题意的图形,并简要说明.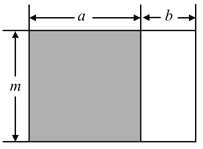
-
科目: 来源: 题型:
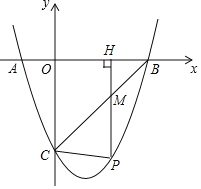
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:
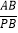 =
=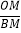 ;
;(3)若AO=2
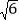 ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.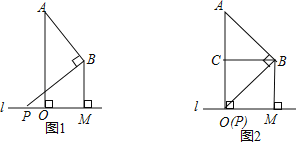
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,G是它的重心,AG⊥CD,如果
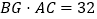 ,则△AGC的面积的最大值是( )
,则△AGC的面积的最大值是( )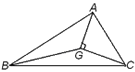
A.
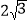 B. 8 C.
B. 8 C. 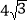 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=_______.

-
科目: 来源: 题型:
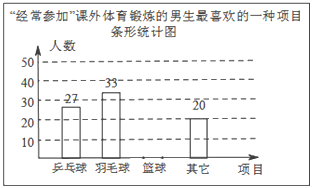
查看答案和解析>>【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如图两幅尚不完整的统计图.请根据以上信息解答下列问题:
①课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为_________.
②请补全条形统计图.
③该校共有1500名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数.

相关试题

