搜索
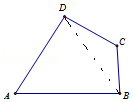
【题目】如图，A，B，C，D为平面四边形ABCD的四个内角，若A+C=180°，AB=6，BC=4，CD=5，AD=5，则四边形ABCD面积是 ． 
参考答案：
【答案】10 
【解析】解：连结BD， 在△ABD中，BD2=AB2+AD2﹣2ABADcosA=61﹣60cosA，
在△BCD中，BD2=BC2+CD2﹣2BCCDcosC=41﹣40cosC．
∴61﹣60cosA=41﹣40cosC，
∵A+C=180°，
∴cosA=﹣cosC．
∴cosA= 
．
∴sinA=sinC= 
．
∴四边形ABCD的面积S=S△ABD+S△BCD= 
AB×AD×sinA+ BC×CD×sinC
= 
6×5× + ×4×5× =10
所以答案是：10 
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知Rt△ABC，AB=3，BC=4，CA=5，P为△ABC外接圆上的一动点，且
的最大值是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知四棱锥P﹣ABCD，底面ABCD为矩形，点E，F在侧棱PA，PB上且PE=2EA，PF=2FB，点M为四棱锥内任一点，则M在平面EFCD上方的概率是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知f（x）=x2（1nx﹣a）+a，则下列结论中错误的是（ ）
A.a＞0，x＞0，f（x）≥0
B.a＞0，x＞0，f（x）≤0
C.a＞0，x＞0，f（x）≥0
D.a＞0，x＞0，f（x）≤0 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆：（x+cosθ）2+（y﹣sinθ）2=1，直线l：y=kx．给出下面四个命题： ①对任意实数k和θ，直线l和圆M有公共点；
②对任意实数k，必存在实数θ，使得直线l和圆M相切；
③对任意实数θ，必存在实数k，使得直线l和圆M相切；
④存在实数k和θ，使得圆M上有一点到直线l的距离为3．
其中正确的命题是（写出所以正确命题的编号） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列{an}满足
，（n∈N+）． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）设
，数列{bn}的前n项和Sn ， 求证： 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】哈六中在2017年3月中旬举办了一次知识竞赛，经过层层筛选，最后五名同学进入了总决赛．在进行笔答题知识竞赛中，最后一个大题是选做题，要求参加竞赛的五名选手从2道题中选做一道进行解答，假设这5位选手选做每一题的可能性均为
． （Ⅰ）求其中甲乙2位选手选做同一道题的概率．
（Ⅱ）设这5位选手中选做第1题的人数为X，求X的分布列及数学期望．
相关试题
