搜索
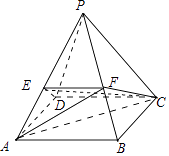
【题目】已知四棱锥P﹣ABCD，底面ABCD为矩形，点E，F在侧棱PA，PB上且PE=2EA，PF=2FB，点M为四棱锥内任一点，则M在平面EFCD上方的概率是（ ）
A.
B.
C.
D.
参考答案：
【答案】B
【解析】解：如图，设四棱锥P﹣ABCD的高为h，底面ABCD的面积为S， ∴ 
．
∵PE=2EA，PF=2FB，
∴EF∥AB，则EF∥平面ABCD，且F到平面ABCD的距离为 
，
∴ 
，
， 
= 
．
则多面体ABCDEF的体积为 
．
∴ 
．
∴M在平面EFCD上方的概率是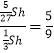 
．
故选：B．
【考点精析】本题主要考查了几何概型的相关知识点，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义在R上的奇函数f（x）满足f（x+1）=f（﹣x），当x∈（0，
]时，f（x）= 
（1﹣x），则f（x）在区间（1， 
）内是（ ）
A.减函数且f（x）＞0
B.减函数且f（x）＜0
C.增函数且f（x）＞0
D.增函数且f（x）＜0 -
科目： 来源： 题型：
查看答案和解析>>【题目】执行右面的程序框图，如果输出的a值大于2017，那么判断框内的条件为（ ）
A.k＜9？
B.k≥9？
C.k＜10？
D.k≥11？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知Rt△ABC，AB=3，BC=4，CA=5，P为△ABC外接圆上的一动点，且
的最大值是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知f（x）=x2（1nx﹣a）+a，则下列结论中错误的是（ ）
A.a＞0，x＞0，f（x）≥0
B.a＞0，x＞0，f（x）≤0
C.a＞0，x＞0，f（x）≥0
D.a＞0，x＞0，f（x）≤0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，B，C，D为平面四边形ABCD的四个内角，若A+C=180°，AB=6，BC=4，CD=5，AD=5，则四边形ABCD面积是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆：（x+cosθ）2+（y﹣sinθ）2=1，直线l：y=kx．给出下面四个命题： ①对任意实数k和θ，直线l和圆M有公共点；
②对任意实数k，必存在实数θ，使得直线l和圆M相切；
③对任意实数θ，必存在实数k，使得直线l和圆M相切；
④存在实数k和θ，使得圆M上有一点到直线l的距离为3．
其中正确的命题是（写出所以正确命题的编号）
相关试题
