【题目】已知Rt△ABC,AB=3,BC=4,CA=5,P为△ABC外接圆上的一动点,且 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:以AC的中点为原点,以ACx轴,建立如图所示的平面直角坐标系,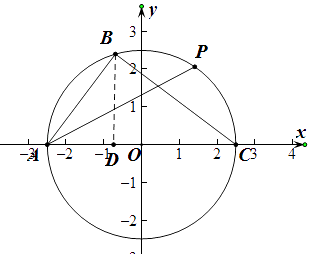
则△ABC外接圆的方程为x2+y2=2.52 ,
设P的坐标为( ![]() cosθ,
cosθ, ![]() sinθ),
sinθ),
过点B作BD垂直x轴,
∵sinA= ![]() ,AB=3
,AB=3
∴BD=ABsinA= ![]() ,AD=ABcosA=
,AD=ABcosA= ![]() ×3=
×3= ![]() ,
,
∴OD=AO﹣AD=2.5﹣ ![]() =
= ![]() ,
,
∴B(﹣ ![]() ,
, ![]() ),
),
∵A(﹣ ![]() ,0),C(
,0),C( ![]() ,0)
,0)
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(5,0),
=(5,0), ![]() =(
=( ![]() cosθ+
cosθ+ ![]() ,
, ![]() sinθ)
sinθ)
∵ ![]() =x
=x ![]() +y
+y ![]()
∴( ![]() cosθ+
cosθ+ ![]() ,
, ![]() sinθ)=x(
sinθ)=x( ![]() ,
, ![]() )+y(5,0)=(
)+y(5,0)=( ![]() x+5y,
x+5y, ![]() x)
x)
∴ ![]() cosθ+
cosθ+ ![]() =
= ![]() x+5y,
x+5y, ![]() sinθ=
sinθ= ![]() x,
x,
∴y= ![]() cosθ﹣
cosθ﹣ ![]() sinθ+
sinθ+ ![]() ,x=
,x= ![]() sinθ,
sinθ,
∴x+y= ![]() cosθ+
cosθ+ ![]() sinθ+
sinθ+ ![]() =
= ![]() sin(θ+φ)+
sin(θ+φ)+ ![]() ,其中sinφ=
,其中sinφ= ![]() ,cosφ=
,cosφ= ![]() ,
,
当sin(θ+φ)=1时,x+y有最大值,最大值为 ![]() +
+ ![]() =
= ![]() ,
,
故选:B
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.
-
科目: 来源: 题型:
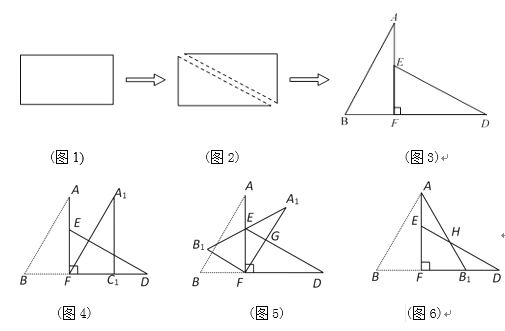
查看答案和解析>>【题目】如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较短直角边长为5cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示),小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的奇函数f(x)满足f(x+1)=f(﹣x),当x∈(0,
 ]时,f(x)=
]时,f(x)=  (1﹣x),则f(x)在区间(1,
(1﹣x),则f(x)在区间(1,  )内是( )
)内是( )
A.减函数且f(x)>0
B.减函数且f(x)<0
C.增函数且f(x)>0
D.增函数且f(x)<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】执行右面的程序框图,如果输出的a值大于2017,那么判断框内的条件为( )

A.k<9?
B.k≥9?
C.k<10?
D.k≥11? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥P﹣ABCD,底面ABCD为矩形,点E,F在侧棱PA,PB上且PE=2EA,PF=2FB,点M为四棱锥内任一点,则M在平面EFCD上方的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=x2(1nx﹣a)+a,则下列结论中错误的是( )
A.a>0,x>0,f(x)≥0
B.a>0,x>0,f(x)≤0
C.a>0,x>0,f(x)≥0
D.a>0,x>0,f(x)≤0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是 .

相关试题

