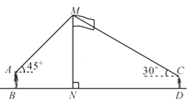
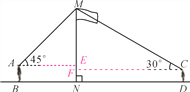
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
参考答案:
【答案】旗杆MN的高度约为13米.
【解析】试题分析:本题主要考查三角函数和解直角三角形,根据题意作点A,C分别向MN作垂线构造两个直角三角形,利用公共边结合三角函数关系进行表示,建立等量关系式列方程求解.
过A作AE⊥MN,垂足为E,过C作CF⊥MN,垂足为F.
设ME=x,Rt△AME中,∠MAE=45°,
∴AE=ME=x,
Rt△MCF中,MF=x+0.2,
CF=![]() =
=![]() (x+0.2),
(x+0.2),
∵BD=AE+CF,
∴x+![]() (x+0.2)=30,
(x+0.2)=30,
∴x≈11,即AE=11,
∴MN=11+1.7=12.7≈13(米),
故旗杆MN的高度约为13米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点A、B分别在函数y1=
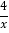 (x>0)与y2=
(x>0)与y2=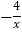 (x<0)的图象上,A、B的横坐标分别为a、b.
(x<0)的图象上,A、B的横坐标分别为a、b.(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b
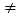 0,求ab的值;
0,求ab的值;(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=
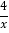 (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为边CD上一点,将
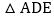 沿AE折叠至
沿AE折叠至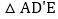 处,
处,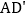 与CE交于点
与CE交于点 若
若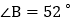 ,
,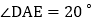 ,则
,则 的大小为________.
的大小为________. 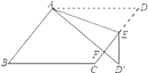
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进入初四后,某科6次考试成绩如图:
(1)请根据下图填写如表:
平均数
方差
中位数
众数
极差
甲
75
75
乙
33.3
15
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形
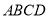 中,
中,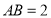 ,
,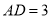 .延长
.延长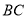 到点
到点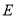 ,使
,使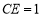 ,连接
,连接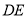 ,动点
,动点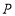 从点
从点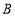 出发,以每秒2个单位的速度沿
出发,以每秒2个单位的速度沿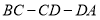 向终点
向终点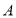 运动,设点
运动,设点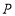 的运动时间为
的运动时间为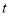 秒,当
秒,当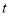 的值为___________时,
的值为___________时,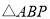 和
和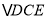 全等.
全等.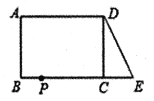
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶
 ,AB=10米,AE=15米(i=1∶
,AB=10米,AE=15米(i=1∶ 是指坡面的铅直高度BH与水平长度AH的比).
是指坡面的铅直高度BH与水平长度AH的比).
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:
 ≈1.414,
≈1.414, ≈1.732)
≈1.732)
相关试题

