【题目】平面直角坐标系xOy中,点A、B分别在函数y1=![]() (x>0)与y2=
(x>0)与y2=![]() (x<0)的图象上,A、B的横坐标分别为a、b.
(x<0)的图象上,A、B的横坐标分别为a、b.
(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b![]() 0,求ab的值;
0,求ab的值;
(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=![]() (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由.

参考答案:
【答案】(1)S△OAB=4;(2)ab=﹣4;(3)见解析.
【解析】
(1)如图1,AB交y轴于C,由于AB∥x轴,根据k的几何意义得到S△OAC=2,S△OBC=2,所以S△OAB=S△OAC+S△OBC=4;
(2)根据函数图象上点的坐标特征得A、B的纵坐标分别为![]() ,根据两点间的距离公式得到
,根据两点间的距离公式得到![]() ,则利用等腰三角形的性质得到a2+(
,则利用等腰三角形的性质得到a2+(![]() )2=b2+(﹣
)2=b2+(﹣![]() )2,变形得到(a+b)(a﹣b)(1﹣
)2,变形得到(a+b)(a﹣b)(1﹣![]() )=0,由于a+b≠0,a>0,b<0,所以1﹣
)=0,由于a+b≠0,a>0,b<0,所以1﹣![]() =0,易得ab=﹣4;
=0,易得ab=﹣4;
(3)由于a≥4,AC=3,则可判断直线CD在y轴的右侧,直线CD与函数y1=![]() (x>0)的图象一定有交点,设直线CD与函数y1=
(x>0)的图象一定有交点,设直线CD与函数y1=![]() (x>0)的图象交点为F,由于A点坐标为(a,
(x>0)的图象交点为F,由于A点坐标为(a,![]() ),正方形ACDE的边长为3,则得到C点坐标为(a﹣3,
),正方形ACDE的边长为3,则得到C点坐标为(a﹣3,![]() ),F点的坐标为(a﹣3,
),F点的坐标为(a﹣3,![]() ),所以FC=
),所以FC=![]() ,然后比较FC与3的大小,由于3﹣FC=3﹣
,然后比较FC与3的大小,由于3﹣FC=3﹣![]() ,而a≥4,所以3﹣FC≥0,于是可判断点F在线段DC上.
,而a≥4,所以3﹣FC≥0,于是可判断点F在线段DC上.
解:(1)如图,AB交y轴于P,
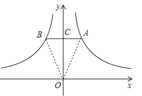
∵AB∥x轴,
∴S△OAC=![]() ×|4|=2,S△OBC=
×|4|=2,S△OBC=![]() ×|﹣4|=2,
×|﹣4|=2,
∴S△OAB=S△OAC+S△OBC=4;
(2)∵A、B的横坐标分别为a、b,
∴OA2=a2+(![]() )2,OB2=b2+(﹣
)2,OB2=b2+(﹣![]() )2,
)2,
∵△OAB是以AB为底边的等腰三角形,
∴OA=OB,
∴a2+(![]() )2=b2+(﹣
)2=b2+(﹣![]() )2
)2
∴(a+b)(a﹣b)(1﹣![]() )=0,
)=0,
∵a+b≠0,a>0,b<0,
∴1﹣![]() =0,
=0,
∴ab=﹣4
(3)∵a≥4,而AC=3,
∴直线CD在y轴的右侧,直线CD与函数y1=![]() (x>0)的图象一定有交点,
(x>0)的图象一定有交点,
设直线CD与函数y1=![]() (x>0)的图象交点为F,如图,
(x>0)的图象交点为F,如图,
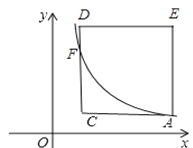
∵A点坐标为(a,![]() ),正方形ACDE的边长为3,
),正方形ACDE的边长为3,
∴C点坐标为(a﹣3,![]() ),
),
∴F点的坐标为(a﹣3,![]() ),
),
∴FC=![]() ﹣
﹣![]()
∵3﹣FC=3﹣![]() ,
,
而a≥4,
∴3﹣FC≥0,即FC≤3,
∵CD=3,
∴点F在线段DC上,
即对大于或等于4的任意实数a,CD边与函数y1=![]() (x>0)的图象都有交点
(x>0)的图象都有交点
-
科目: 来源: 题型:
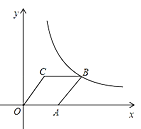
查看答案和解析>>【题目】如图,菱形OABC的顶点C的坐标为(6,8).顶点A在x轴的正半轴上,反比例函数
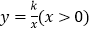 的图象经过顶B点.
的图象经过顶B点.(1)求点A和B的坐标;
(2)求k值及直线AB对应的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游,不同租赁公司的租车费用(单位:元)与时间(单位:
 )之间的关系如图所示.
)之间的关系如图所示.
根据以上信息,解答下列问题:
(1)设租车时间为
 时,租用甲公司的车所需费用为
时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数解析式;
的函数解析式;(2)请你帮助小明计算并选择哪个出游方案合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为边CD上一点,将
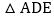 沿AE折叠至
沿AE折叠至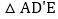 处,
处,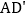 与CE交于点
与CE交于点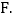 若
若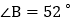 ,
,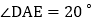 ,则
,则 的大小为________.
的大小为________. 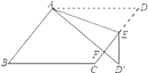
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:
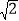 ≈1.414,
≈1.414,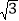 ≈1.732,结果保留整数)
≈1.732,结果保留整数)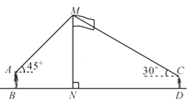
相关试题

