【题目】如图,已知直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.

(1)k的值为 ;当x的取值范围为 时,y1>y2;
(2)若双曲线y2=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.
参考答案:
【答案】(1)8、x>4或﹣4<x<0;(2)15
【解析】
试题分析:(1)根据正比例函数先求出点A的坐标,从而求出了k值为8,然后通过解方程组求得B的坐标,根据图象即可求得y1>y2时的x的取值.;
(2)过A、C点分别作x轴、y轴的垂线垂足为G、E,两垂线交于点F,则四边形EFGO是矩形,根据C的纵坐标求得C的坐标,然后根据S△AOC=S矩形﹣SOEC﹣S△CFA﹣S△OAG计算即可.
解:(1)∵点A横坐标为4,
∴由y1=![]() x可知当x=4时,y=2.
x可知当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)的交点,
(k>0)的交点,
∴k=4×2=8.
∴双曲线的解析式为y=![]() ,
,
解![]() 得
得![]() 或
或![]() ,
,
∴A((4,2),B(﹣4,﹣2),
根据图象可知:当x>4或﹣4<x<0时,y1>y2;
故答案为8、x>4或﹣4<x<0.
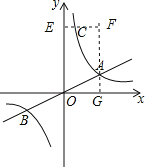
(2)如图,过A、C点分别作x轴、y轴的垂线垂足为G、E,两垂线交于点F,则四边形EFGO是矩形,
∵点C在双曲线上,点C的纵坐标为8,
∴8=![]() ,解得x=1,
,解得x=1,
∴C(1,8),
∴S△AOC=S矩形﹣SOEC﹣S△CFA﹣S△OAG=8×4﹣![]() ×1×8﹣
×1×8﹣![]() (4﹣1)×(8﹣2)﹣
(4﹣1)×(8﹣2)﹣![]() ×4×2=32﹣4﹣9﹣4=15.
×4×2=32﹣4﹣9﹣4=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长沙红星大市场某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
A.562.5元 B.875元 C.550元 D.750元
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
318
652
793
1604
4005
发芽频率
0.850
0.795
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.10).
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)请用两种不同的方法,求图b中阴影部分的面积:
方法1: ; 方法2: ;
(2)观察图b,写出代数式
 ,
,  ,
,  之间的等量关系,并通过计算验证;
之间的等量关系,并通过计算验证;(3)根据(2)题中的等量关系,解决如下问题:若
 ,
,  ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
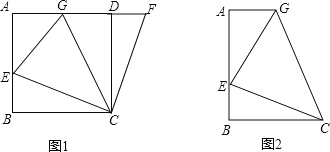
(1)①试说明CE=CF,∠BCE=∠DCF;
②如图1,若点G在AD上,且∠GCE=45°,则GE=GF成立吗?为什么?
(2)运用(1)中积累的经验和知识,完成下题:
如图2,在梯形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=6,E是AB上 一点,且∠GCE=45°,BE=2,求GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳计算结果中的个位数字的规律,猜测32015﹣1的个位数字是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:|a﹣1|+|b+2|=0,求2a+b的值.
相关试题

