【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
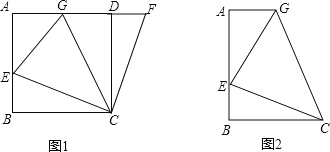
(1)①试说明CE=CF,∠BCE=∠DCF;
②如图1,若点G在AD上,且∠GCE=45°,则GE=GF成立吗?为什么?
(2)运用(1)中积累的经验和知识,完成下题:
如图2,在梯形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=6,E是AB上 一点,且∠GCE=45°,BE=2,求GE的长.
参考答案:
【答案】(1)成立(2)GE=5
【解析】
试题分析:(1)①根据正方形的性质可得BC=CD,再利用“边角边”证明△BCE和△DCF全等,根据全等三角形对应边相等、对应角相等的单结论;
②根据全等三角形对应角相等可得∠BCE=∠DCF,再求出∠GCF=45°,从而得到∠GCF=∠GCE,再利用“边角边”证明△GCE和△GCF全等,根据全等三角形对应边相等可得EG=GF;
(2)设EG=x,根据(1)的结论表示出AG,再求出AE,然后在Rt△AEG中,利用勾股定理列出方程求解即可.
(1)①证明:在正方形ABCD中,BC=CD,
在△BCE和△DCF中,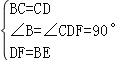 ,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;,∠BCE=∠DCF
②EG=BE+GD.
理由如下:∵△BCE≌△DCF,
∴∠BCE=∠DCF,
∵∠GCE=45°,
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=90°﹣45°=45°,
∴∠GCF=∠GCE,
在△GCE和△GCF中,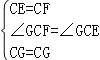 ,
,
∴△GCE≌△GCF(SAS),
∴EG=GF;
(2)设EG=x,
由(1)可知,BE+(6﹣AG)=EG,
即2+(6﹣AG)=x,
∴AG=8﹣x,
又∵AE=AB﹣BE=6﹣2=4,
∴在Rt△AEG中,AE2+AG2=EG2,
即42+(8﹣x)2=x2,
解得x=5,
即GE=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
318
652
793
1604
4005
发芽频率
0.850
0.795
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.10).
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)请用两种不同的方法,求图b中阴影部分的面积:
方法1: ; 方法2: ;
(2)观察图b,写出代数式
 ,
,  ,
,  之间的等量关系,并通过计算验证;
之间的等量关系,并通过计算验证;(3)根据(2)题中的等量关系,解决如下问题:若
 ,
,  ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y1=
 x与双曲线y2=
x与双曲线y2=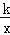 (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.
(1)k的值为 ;当x的取值范围为 时,y1>y2;
(2)若双曲线y2=
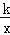 (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳计算结果中的个位数字的规律,猜测32015﹣1的个位数字是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:|a﹣1|+|b+2|=0,求2a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校机房今年和去年共购置了100台计算机,已知今年购置计算机数量是去年购置计算机数量的3倍,今年购置计算机的数量是( )
A.25台 B.50台 C.75台 D.100台
相关试题

