搜索
【题目】魔方，又叫魔术方块，也称鲁比克方块,是匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授在1974年发明的。魔方与中国人发明的“华容道”，法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议。如图是一个4阶魔方，又称“魔方的复仇”，由四层完全相同的64个小立方体组成，体积为64
．
(1)求组成这个魔方的小立方体的棱长.
（2）图中阴影部分是一个正方形，则该阴影部分正方形的面积为_________ 
. 边长是___________ 
.
参考答案：
【答案】（1）1cm；（2）
； 
【解析】试题分析：（1）先求1个小立方体的体积为64÷64=1cm3，再开立方就是小立方体的棱长；
（2）根据勾股定理可求得阴影部分的边长，平方后就是面积．
试题解析：：（1）棱长=
，
答：组成这个魔方的小立方体的棱长为1cm；
（2）由勾股定理得：阴影部分正方形的边长=
，
面积=（
）2=10，
-
科目： 来源： 题型：
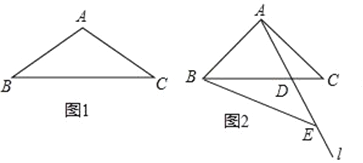
查看答案和解析>>【题目】钝角三角形ABC中，∠BAC＞90°，AB=AC，∠ACB=α，过点A的直线l交BC边于点D．点E在直线l上，且BC=BE．，点E在AD延长线上．
①当α=30°，点D恰好为BC中点时，补全图1直接写出∠BAE= °，
∠BEA= °；
②如图2，若∠BAE=2α，求∠BEA的度数（用含α的代数式表示）；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，△AOB为等腰直角三角形，A（4，4）
（1）求B点坐标；
（2）如图2，若C为x正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=90°，连接OD，求∠AOD的度数；
（3）如图3，过点A作y轴的垂线交y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连FM，等式AM=FM+OF是否成立？若成立，请说明；若不成立，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠A +∠B +∠C +∠D +∠E +∠F等于（ ）
A. 180° B. 360° C. 540° D. 720°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB边的垂直平分线
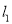交BC于D，AC边的垂直平分线
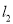交BC于E， 
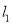与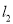
相交于点O，△ADE的周长为6cm．（1）求BC的长；
（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；
-
科目： 来源： 题型：
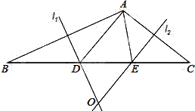
查看答案和解析>>【题目】如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC，AB与EC交于点D．问：
（1）EC与BF有什么大小关系？并说明理由.
（2）EC与BF的位置关系是__________.（直接写出结论，不证明）
-
科目： 来源： 题型：
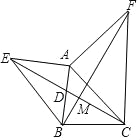
查看答案和解析>>【题目】（1）如图1，∠MAN=90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．求证：△ABD≌△CAF；
（2）如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC．求证：△ABE≌△CAF；
（3）如图3，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，求△ACF与△BDE的面积之和．
相关试题
