【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)△ACF与△BDE的面积之和5.
【解析】如图①,求出∠BDA=∠AFC=90°,∠ABD=∠CAF,根据AAS证两三角形全等即可;图②根据已知和三角形外角性质求出∠ABE=∠CAF,∠BAE=∠FCA,根据ASA证两三角形全等即可;图③求出△ABD的面积,根据△ABE≌△CAF得出△ACF与△BDE的面积之和等于△ABD的面积,即可得出答案.
证明:如图①,

∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∠ADB=∠CFA,∠ABD=∠CAF,AB=AC,
∴△ABD≌△CAF(AAS);
(2)∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∠ABE=∠CAF,AB=AC,∠BAE=∠FCA,
∴△ABE≌△CAF(ASA);
(3)∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是: ![]() ×15=5,
×15=5,
由(2)中证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积,是5.
“点睛”本题考查了全等三角形的性质和判定,三角形的面积,三角形的外角性质等知识点,主要考查学生的分析问题和解决问题的能力,题目比较典型,证明过程有类似之处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,互为相反数的是( )
A.﹣(﹣1)与1
B.(﹣1)2与1
C.|﹣1|与1
D.﹣12与1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形中求角度,如果己知等腰三角形的一个内角,求其底角的度数,需要分为已知角是等腰三角形的顶角或者底角两种情况,这体现的数学思想是( )
A.数形结合B.类比思想
C.分类讨论D.公理化
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师给同学们布置了以下解方程的作业,作业要求是无实数根的方程不用解,不用解的方程是( )
A.x2﹣x=0B.x2+x=0C.x2+x﹣1=0D.x2+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】请通过计算推测32017的个位数是
A. 1 B. 3
C. 7 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=3x2向左平移2个单位,再向上平移1个单位,所得的抛物线的解析式是 .
-
科目: 来源: 题型:
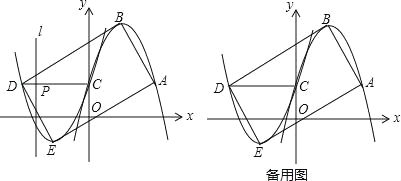
查看答案和解析>>【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
相关试题

