【题目】把两个全等的等腰直角三角板(直角边长为4)叠放在一起,且三角板EFG的直角顶点G位于三角板ABC的斜边中点处.现将三角板EFG绕G点按顺时针方向旋转α度(0°<α<90°)(如图1),四边形GKCH为两三角板的重叠部分.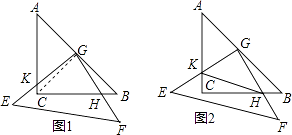
(1)猜想BH与CK有怎样的数量关系?并证明你的结论;
(2)连接HK(如图2),在上述旋转过程中,设BH=x,△GKH的面积为y,
①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当△GKH的面积恰好等于△ABC面积的 ![]() ,求x.
,求x.
参考答案:
【答案】
(1)
解:BH=CK.
理由如下:∵点O是等腰直角三角板ABC斜边中点,
∴∠B=∠GCK=45°,BG=CG,
由旋转的性质,知∠BGH=∠CGK,
在△BGH和△CGK中,
 ,
,
∴△BGH≌△CGK(ASA),
∴BH=CK;
(2)
解:①∵△BGH≌△CGK,
∴S四边形CHGK=S△CGK+S△CGH=S△BGH+S△CGH=S△BCG= ![]() S△ABC=4,
S△ABC=4,
∴S△GKH=S四边形CHGK﹣S△KCH=4﹣ ![]() CH×CK,
CH×CK,
∴y= ![]() x2﹣2x+4(0<x<4),
x2﹣2x+4(0<x<4),
②当y= ![]() ×8=
×8= ![]() 时,即
时,即 ![]() x2﹣2x+4=
x2﹣2x+4= ![]() ,
,
∴x=1 或x=3.
∴当△GKH的面积恰好等于△ABC面积的 ![]() 时,BH=1 或BH=3.
时,BH=1 或BH=3.
【解析】(1)先由ASA证出△CGK≌△BGH,再根据全等三角形的性质得出BH=CK,根据全等得出四边形CKGH的面积等于三角形ACB面积一半;(2)①由(1)易得S四边形CHGK= ![]() S△ABC , 然后根据面积公式得出y=
S△ABC , 然后根据面积公式得出y= ![]() x2﹣2x+4;②根据△GKH的面积恰好等于△ABC面积的
x2﹣2x+4;②根据△GKH的面积恰好等于△ABC面积的 ![]() ,代入得出方程即可求得结果.
,代入得出方程即可求得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个?
(1)AE平分∠DAB;(2)△EBA≌△DCE; (3)AB+CD=AD;(4)AE⊥DE;(5)AB//CD;
大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F.
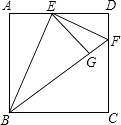
(1)若∠ABE:∠BFC=n,则n=;
(2)当E运动到AD中点时,求线段GF的长;
(3)若限定F仅在线段CD上(含端点)运动,直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【背景】国家为扶持软件企业的发展,对企业实行月补贴,以提高企业的净利润.
【问题】国内某软件企业2014 年12月份并未如期收到700万元的月补贴,这样导致2014 年的净利润增长只有55%.而若补贴及时到位,则2014 年的净利润增长将达到60%.
(1)求2013年该企业净利润是多少万元?
(2)又据统计,2014年12月该企业不含月补贴的月净利润为2100万元,2015年1月及2月不含月补贴的月净利润比上月增加的百分数分别是m和 2m,这两个月的月补贴相等,且都在2014年12月基础上增加了2m.据推算,若以后各月不含月补贴的月净利润和月补贴均稳定在2月份的水平不变,则 2015年该企业净利润将达到2013年的3倍,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:
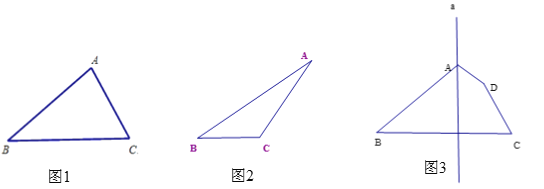
(1)用直尺和圆规作图(不写作法,保留作图痕迹)在图1中,作△ABC的角平分线BD; 在图2中,作△ABC的高AE;
(2)在图3中,画出下列图形关于直线a的对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在平面直角坐标系中.等腰Rt△OAB的斜边OA在x轴上.P为线段OB上﹣动点(不与O,B重合).过P点向x轴作垂线.垂足为C.以PC为边在PC的右侧作正方形PCDM.OP=
 t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
(1)写出t的取值范围 , 写出M的坐标:();
(2)用含a,t的代数式表示b;
(3)当抛物线开向下,且点M恰好运动到AB边上时(如图2)
①求t的值;
②若N在△OAB的内部及边上,试求a及m的取值范围. -
科目: 来源: 题型:
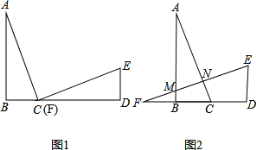
查看答案和解析>>【题目】已知,如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AC=EF,BC=DE .
(1)请说明△ABC≌△FDE,并判断AC是否垂直FE?
(2)若将△ABC 沿BD方向平移至如图2的位置时,且其余条件不变,则AC是否垂直FE?请说明为什么?
相关试题

