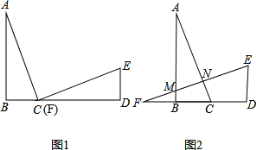
【题目】已知,如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AC=EF,BC=DE .
(1)请说明△ABC≌△FDE,并判断AC是否垂直FE?
(2)若将△ABC 沿BD方向平移至如图2的位置时,且其余条件不变,则AC是否垂直FE?请说明为什么?
参考答案:
【答案】(1)AC⊥EF,理由见解析; (2)AC⊥FE,理由见解析.
【解析】
(1)根据HL的判定方法可证明△ABC≌△FDE,根据两个全等直角三角形的几个锐角之间的关系即可证明AC⊥EF.(2)由(1)可知∠A=∠F,根据∠ABC=∠ABF=90°,∠AMN=∠FMB,可知∠F+∠FMB=90°, ∠A+∠AMN=90°,进而可证明∠ANM=90°,即AC⊥FE.
(1)AC⊥EF.理由如下:
∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,
在Rt△ABC和Rt△FDE中
∵AC=EF,BC=DE
∴△ABC≌△FDE(HL)
∴∠A=∠EFD,
∵∠B=90°,
∴∠A+∠ACB=90°,
∴∠ACB+∠ECD=90°,
∴∠ACE=180°-90°=90°,
∴AC⊥CE,
即AC⊥FE.
(2)AC垂直FE,理由如下:
∵∠A=∠F(已证),∠ABC=∠ABF=90°,∠AMN=∠FMB,
∴∠F+∠FMB=90°,
∴∠A+∠AMN=90°,
∴∠ANM=180°-90°=90°,
∴AC⊥FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把两个全等的等腰直角三角板(直角边长为4)叠放在一起,且三角板EFG的直角顶点G位于三角板ABC的斜边中点处.现将三角板EFG绕G点按顺时针方向旋转α度(0°<α<90°)(如图1),四边形GKCH为两三角板的重叠部分.
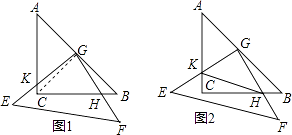
(1)猜想BH与CK有怎样的数量关系?并证明你的结论;
(2)连接HK(如图2),在上述旋转过程中,设BH=x,△GKH的面积为y,
①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当△GKH的面积恰好等于△ABC面积的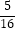 ,求x.
,求x. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:
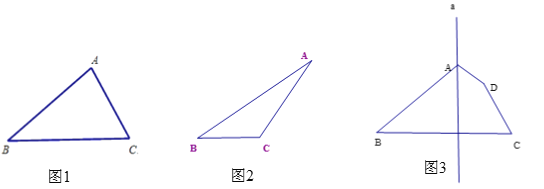
(1)用直尺和圆规作图(不写作法,保留作图痕迹)在图1中,作△ABC的角平分线BD; 在图2中,作△ABC的高AE;
(2)在图3中,画出下列图形关于直线a的对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在平面直角坐标系中.等腰Rt△OAB的斜边OA在x轴上.P为线段OB上﹣动点(不与O,B重合).过P点向x轴作垂线.垂足为C.以PC为边在PC的右侧作正方形PCDM.OP=
 t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
(1)写出t的取值范围 , 写出M的坐标:();
(2)用含a,t的代数式表示b;
(3)当抛物线开向下,且点M恰好运动到AB边上时(如图2)
①求t的值;
②若N在△OAB的内部及边上,试求a及m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在等腰直角△ABC中,∠B=90°,将△ABC绕点 A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
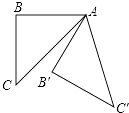
A.105°
B.120°
C.135°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
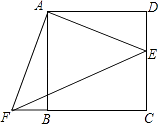
(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
相关试题

