【题目】如图1在平面直角坐标系中.等腰Rt△OAB的斜边OA在x轴上.P为线段OB上﹣动点(不与O,B重合).过P点向x轴作垂线.垂足为C.以PC为边在PC的右侧作正方形PCDM.OP= ![]() t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
(1)写出t的取值范围 , 写出M的坐标:();
(2)用含a,t的代数式表示b;
(3)当抛物线开向下,且点M恰好运动到AB边上时(如图2)
①求t的值;
②若N在△OAB的内部及边上,试求a及m的取值范围.
参考答案:
【答案】
(1)解:0<t< ![]() ;2t,t
;2t,t
(2)
解:把M(2t,t)代入到y=ax2+bx中得:
t=4at2+2tb,
1=4at+2b,
b= ![]() ;
;
(3)
解:①如图2,∵OB= ![]() ,OP=
,OP= ![]() t,
t,
∴PB= ![]() ﹣
﹣ ![]() t,
t,
∵PM∥OA,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t=1;
②由(2)得:b= ![]() =
= ![]() ﹣2a,即4a=1﹣2b,
﹣2a,即4a=1﹣2b,
顶点N(﹣ ![]() ,﹣
,﹣ ![]() )(a<0,b>0),
)(a<0,b>0),
i)当0≤﹣ ![]() ≤
≤ ![]() 时,即a≤﹣
时,即a≤﹣ ![]() 时,
时,
﹣ ![]() ≥﹣
≥﹣ ![]() ,解得a≥﹣
,解得a≥﹣ ![]() ,
,
∴﹣ ![]() ≤a≤﹣
≤a≤﹣ ![]() ,
,
ii)当 ![]() <﹣
<﹣ ![]() ≤3时,即﹣
≤3时,即﹣ ![]() <a≤﹣
<a≤﹣ ![]() ,
,
3﹣(﹣ ![]() )≥﹣
)≥﹣ ![]() ,
,
b2﹣4b+3≤0,
1≤b≤3,
1≤ ![]() ﹣2a≤3,﹣
﹣2a≤3,﹣ ![]() ≤a≤﹣
≤a≤﹣ ![]() ,
,
则﹣ ![]() <a≤﹣
<a≤﹣ ![]() ,
,
综上所述:a的取值为:﹣ ![]() ≤a≤﹣
≤a≤﹣ ![]() ,
,
m=﹣ ![]() =1﹣
=1﹣ ![]() ,
,
得:4am=4a﹣1,a=﹣ ![]() =
= ![]() ,
,
﹣ ![]() ≤
≤ ![]() ≤﹣
≤﹣ ![]() ,
,
∴ ![]() ≤m≤2.
≤m≤2.
【解析】 解:(1)如图1,∵△OAB为等腰直角三角形,OA=3,
∴OB=AB= ![]() =
= ![]() ,
,
∵P为线段OB上﹣动点(不与O,B重合),
∴0< ![]() t<
t< ![]() ,
,
∴0<t< ![]() ,
,
∵四边形PCDM为正方形,
∴∠PCO=90°,
∵∠POC=45°,
∴△POC为等腰直角三角形,
∵OP= ![]() t,
t,
∴PC=OC=t,
∴OD=t+t=2t,
∴M(2t,t);
【考点精析】掌握二次函数的图象是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【背景】国家为扶持软件企业的发展,对企业实行月补贴,以提高企业的净利润.
【问题】国内某软件企业2014 年12月份并未如期收到700万元的月补贴,这样导致2014 年的净利润增长只有55%.而若补贴及时到位,则2014 年的净利润增长将达到60%.
(1)求2013年该企业净利润是多少万元?
(2)又据统计,2014年12月该企业不含月补贴的月净利润为2100万元,2015年1月及2月不含月补贴的月净利润比上月增加的百分数分别是m和 2m,这两个月的月补贴相等,且都在2014年12月基础上增加了2m.据推算,若以后各月不含月补贴的月净利润和月补贴均稳定在2月份的水平不变,则 2015年该企业净利润将达到2013年的3倍,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把两个全等的等腰直角三角板(直角边长为4)叠放在一起,且三角板EFG的直角顶点G位于三角板ABC的斜边中点处.现将三角板EFG绕G点按顺时针方向旋转α度(0°<α<90°)(如图1),四边形GKCH为两三角板的重叠部分.
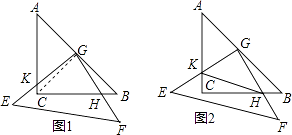
(1)猜想BH与CK有怎样的数量关系?并证明你的结论;
(2)连接HK(如图2),在上述旋转过程中,设BH=x,△GKH的面积为y,
①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当△GKH的面积恰好等于△ABC面积的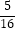 ,求x.
,求x. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:
(1)用直尺和圆规作图(不写作法,保留作图痕迹)在图1中,作△ABC的角平分线BD; 在图2中,作△ABC的高AE;
(2)在图3中,画出下列图形关于直线a的对称图形
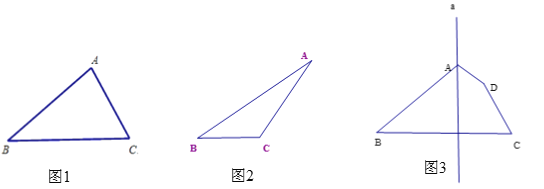
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AC=EF,BC=DE .
(1)请说明△ABC≌△FDE,并判断AC是否垂直FE?
(2)若将△ABC 沿BD方向平移至如图2的位置时,且其余条件不变,则AC是否垂直FE?请说明为什么?
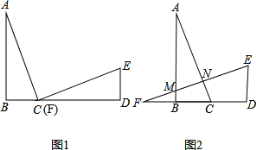
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在等腰直角△ABC中,∠B=90°,将△ABC绕点 A逆时针旋转60°后得到的△AB′C′,则∠BAC′等于( )
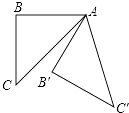
A.105°
B.120°
C.135°
D.150°
相关试题

