【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA.
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
参考答案:
【答案】
(1)
证明:如图1,连接CD,
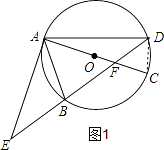
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ADB+∠EDC=90°,
∵∠BAC=∠EDC,∠EAB=∠ADB,
∴∠EAC=∠EAB+∠BAC=90°,
∴EA是⊙O的切线.
(2)
证明:如图2,连接BC,
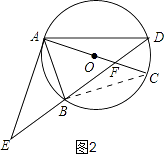
由(1)知,∠EAF=∠EAC=90°,
∵B是EF的中点,
∴在Rt△EAF中,AB=BF(直角三角形斜边的中线等于斜边的一半),
∴∠BAC=∠AFE,
∴△EAF∽△CBA.
(3)
解:∵△EAF∽△CBA,
∴ ![]() ,
,
∵AF=4,CF=2.
∴AC=6,EF=2AB,
∴ ![]() ,解得AB=2
,解得AB=2 ![]() .
.
∴EF=4 ![]() ,
,
在Rt△AEF中,由勾股定理得,AE= ![]() =4
=4 ![]()
【解析】(1)连接CD,由AC是⊙O的直径,可得出∠ADC=90°,由角的关系可得出∠EAC=90°,即得出EA是⊙O的切线,(2)连接BC,由AC是⊙O的直径,可得出∠ABC=90°,由在Rt△EAF中,B是EF的中点,可得出∠BAC=∠AFE,即可得出△EAF∽△CBA,(3))由△EAF∽△CBA,可得出 ![]() ,由比例式可求出AB,由勾股定理得出AE的长.
,由比例式可求出AB,由勾股定理得出AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.

(1)李老师采取的调查方式是(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图2补充完整.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC.

(1)求证:CD=AN;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+b与反比例函数
 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4. 
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒
 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).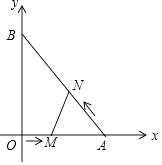
(1)当t=3秒时,直接写出点N的坐标;
(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;
(3)当t为何值时,△MNA是一个等腰三角形? -
科目: 来源: 题型:
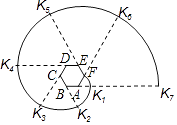
查看答案和解析>>【题目】如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1 , 弧K1K2 , 弧K2K3 , 弧K3K4 , 弧K4K5 , 弧K5K6 , …的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1 , L2 , L3 , L4 , L5 , L6 , ….当AB=1时,L2016等于( )
A.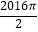
B.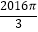
C.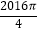
D.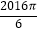 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π).

相关试题

