【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图. 
(1)李老师采取的调查方式是(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图2补充完整.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
参考答案:
【答案】
(1)抽样调查;12;3
(2)解:画树状图如下:
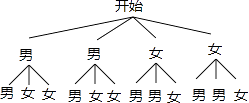
∵所有等可能的情况有12种,其中一男一女有8种,
∴恰好抽中一男一女的概率为: ![]() =
= ![]() .
.
【解析】解:(1)∵李老师所调查的4个班征集到作品共:5÷ ![]() =12(件), ∴B班征集到作品:12﹣2﹣5﹣2=3(件);
=12(件), ∴B班征集到作品:12﹣2﹣5﹣2=3(件);
∴李老师采取的调查方式是抽样调查,李老师所调查的4个班征集到作品共12件,其中B班征集到作品3件,
故答案为:抽样调查;12;3;
补全图2,如图所示: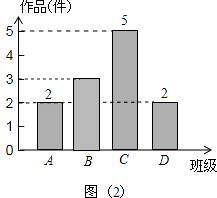
(1)由题意可求得李老师所调查的4个班征集到作品共:5÷ ![]() =12(件),B班征集到作品:12﹣2﹣5﹣2=3(件);继而可补全条形统计图;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中一男一女的情况,再利用概率公式即可求得答案.
=12(件),B班征集到作品:12﹣2﹣5﹣2=3(件);继而可补全条形统计图;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中一男一女的情况,再利用概率公式即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2017﹣
 )0×
)0× 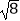 ﹣(
﹣(  )﹣1﹣4cos45°.
)﹣1﹣4cos45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空:
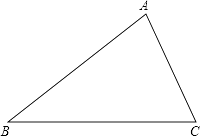
(1)作∠ABC的平分线BD交AC于点D;
(2)作线段BD的垂直平分线交AB于点E,交BC于点F.由(1)、(2)可得:线段EF与线段BD的关系为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC.

(1)求证:CD=AN;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+b与反比例函数
 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4. 
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.

(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA.
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
相关试题

