【题目】如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒 ![]() 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).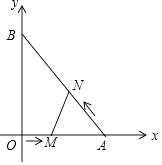
(1)当t=3秒时,直接写出点N的坐标;
(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;
(3)当t为何值时,△MNA是一个等腰三角形?
参考答案:
【答案】
(1)
解:作NC⊥OA于C,
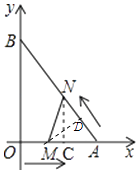
∵t=3时,AN=3× ![]() =5,
=5,
∴CN=ANsin∠OAB=5× ![]() =4,AC=ANcos∠OAB=5×
=4,AC=ANcos∠OAB=5× ![]() =3,
=3,
∴OC=OA﹣AC=3,
∴N(3,4)
故答案为N(3,4).
(2)
解:由题意,AN= ![]() t,AM=OA﹣OM=6﹣t,
t,AM=OA﹣OM=6﹣t,
NC=NAsin∠BAO= ![]() t
t ![]() =
= ![]() t,
t,
则:S△MNA= ![]() AMNC=
AMNC= ![]() ×(6﹣t)×
×(6﹣t)× ![]() t,
t,
=﹣ ![]() (t﹣3)2+6.
(t﹣3)2+6.
∴△MNA的面积有最大值,且最大值为6.
(3)
解:(解法1)AM=6﹣t,AN= ![]() t (0<t<6),
t (0<t<6),
∴AC=ANcos∠BAO=t,
①当AM=AN时,6﹣t= ![]() t,即 t=
t,即 t= ![]() ,
,
②当MN=AN时,则NC垂直平分线段MA,
∴MC=AC=t
∵OM+MC+CA=OA
∴t+t+t=6 解得t=2
③当MN=MA时,设D为线段AN的中点,则 MD垂直平分线段AN
∴AD= ![]() AN=
AN= ![]() ,
,
又∵cos∠DAM=cos∠OAB (或∵△DAM∽△OAB)
∴ ![]() 即
即 ![]() 解得 t=
解得 t= ![]() .
.
综上,当t的值取 2或 ![]() 或
或 ![]() 时,△MAN是等腰三角形.
时,△MAN是等腰三角形.
(解法2)AN= ![]() t,NC=
t,NC= ![]() t,AC=ANcos∠BAO=t;
t,AC=ANcos∠BAO=t;
∴OC=OA﹣AC=6﹣t,
∴MC=|OC﹣OM|=|6﹣t﹣t|=|6﹣2t|
Rt△NCM中 NM2=MC2+NC2
∴NM= ![]() =
= ![]() ,
,
∴ ![]() ,
,
又:AM=6﹣t,AN= ![]() t(0<t<6);
t(0<t<6);
①当MN=AN时,MN2=AN2
∴ ![]() =
= ![]() ,
,
即:t2﹣8t+12=0,t1=2,t2=6(舍去);
②当MN=MA时,MN2=MA2
∴ ![]() =(6﹣t)2,
=(6﹣t)2,
即: ![]() t2﹣12t=0,t1=0(舍去),t2=
t2﹣12t=0,t1=0(舍去),t2= ![]() ;
;
③当AM=AN时,6﹣t= ![]() t,即t=
t,即t= ![]() ;
;
综上,当t的值取 2或 ![]() 或
或 ![]() 时,△MAN是等腰三角形.
时,△MAN是等腰三角形.
【解析】(1)作NC⊥OA于C,在Rt△ANC中,求出NC、AC即可解决问题;(2)过点N作NC⊥OA于C.由题意,AN= ![]() t,AM=OA﹣OM=6﹣t,NC=NAsin∠BAO=
t,AM=OA﹣OM=6﹣t,NC=NAsin∠BAO= ![]() t
t ![]() =
= ![]() t,则:S△MNA=
t,则:S△MNA= ![]() AMNC=
AMNC= ![]() ×(6﹣t)×
×(6﹣t)× ![]() t=﹣
t=﹣ ![]() (t﹣3)2+6,根据二次函数的性质即可解决问题;(3)分三种情形方程列出方程即可解决问题..
(t﹣3)2+6,根据二次函数的性质即可解决问题;(3)分三种情形方程列出方程即可解决问题..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC.

(1)求证:CD=AN;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+b与反比例函数
 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4. 
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.

(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA.
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1 , 弧K1K2 , 弧K2K3 , 弧K3K4 , 弧K4K5 , 弧K5K6 , …的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1 , L2 , L3 , L4 , L5 , L6 , ….当AB=1时,L2016等于( )
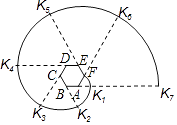
A.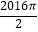
B.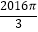
C.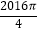
D.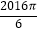 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3.14﹣π)0+|1﹣
 |+(﹣
|+(﹣  )﹣1﹣2sin60°.
)﹣1﹣2sin60°.
相关试题

