【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C,(﹣1,﹣2),D(1,﹣2),点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为_____.

参考答案:
【答案】(﹣1,﹣1).
【解析】
由点A、B、C、D的坐标可得出AB、BC的长度,设点M和点N第2017次相遇时的时间为x,根据第一次相遇的路程和=周长,所以第2017次相遇的路程和=周长×2017,即可得出关于x的一元一次方程,解之即可得出x的值,再根据路程=速度×时间可求出M和点N第2017次相遇时,点M走过的路程,结合矩形的周长为12,即可找出点M和点N第2017次相遇时的坐标,此题得解.
解:∵A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2),
∴AB=2,BC=4.
设点M和点N第2017次相遇时的时间为x,
根据题意得:(1+2)x=2017×2×(4+2),
解得:x=8068,
∴M和点N第2017次相遇时,点M走过的路程为x=8068.
∵矩形ABCD的周长为12,8068=672×12+4,
∴M和点N第2017次相遇时的位置在距离点E逆时针方向的4个单位长度.
∵BC=4,BE=1,
∴点M和点N第2017次相遇时的位置为线段CF的中点,即点(﹣1,﹣1).
故答案为:(﹣1,﹣1).
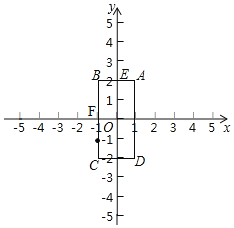
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.

(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, ,若动点P从点C开始,按
,若动点P从点C开始,按 的路径运动,且速度为每秒1cm,设出发的时间为t秒.
的路径运动,且速度为每秒1cm,设出发的时间为t秒.
 出发2秒后,求
出发2秒后,求 的面积;
的面积; 当t为几秒时,BP平分
当t为几秒时,BP平分 ;
; 问t为何值时,
问t为何值时, 为等腰三角形?
为等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中.
(1)写出点A,点B的坐标A( , ),B( , );
(2)S△ABC= ;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1的位置,并写出点A1、B1、C1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°.
(1)用圆规和直尺在AC上作点P,使点P到A、B的距离相等.(保留作图痕迹,不写作法和证明)
(2)当满足(1)的点P到AB、BC的距离相等时,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 来表示
来表示 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为
 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:(1)若
 的整数部分为
的整数部分为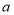 ,小数部分为
,小数部分为 ,求
,求 的值.
的值.(2)已知:
 ,其中
,其中 是整数,且
是整数,且 ,求
,求 的值.
的值.
相关试题

