【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)【探索体验】如图1,已知在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.求证:四边形ABCD是“等对角四边形”.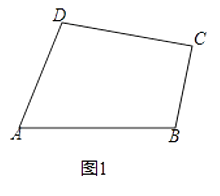
(2)如图2,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.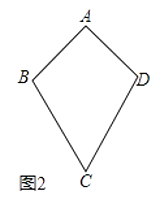
(3)【尝试应用】如图3,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4m,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.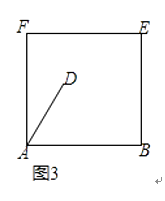
参考答案:
【答案】
(1)证明:∵在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.
∴∠D=360°﹣∠A﹣∠B﹣∠C=100°,∠A≠∠C,
∴∠D=∠D,
∴四边形ABCD是“等对角四边形”
(2)证明:如图2,连接BD,
∵AB=AD,CB=CD,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∴∠ABD+∠CBD=∠ADB+∠CDB,
∴∠ABC=∠ADC,
∵AB=AD=a,CB=CD=b,且a≠b,且BD=BD,
∴△ABD与△CBD不相似,
∴∠A≠∠C,
∴四边形ABCD是“等对角四边形”
(3)如图3,连接BD,
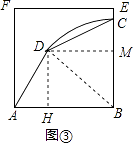
当∠DAB=∠BCD=60°时,四边形ABCD是“等对角四边形”,
此时点C在BD为弦的 ![]() 上,
上,
要使四边形ABCD的面积最大,则点C在边BE上,
过点D作DH⊥AB于点H,作DM⊥BC于点M,
在Rt△ADH中,∠DAH=60°,AD=4,
∴AH=2,DH=2 ![]() ,
,
∴BH=AB﹣AH=4,
∵四边形DHBM是矩形,
∴BM=DH=2 ![]() ,DM=BH=4,
,DM=BH=4,
在Rt△DMC中,∠DCM=60°,
∴CM= ![]() DM=
DM= ![]() ,
,
∴BC=BM+CM=2 ![]() +
+ ![]() =
= ![]() ,
,
∴S四边形ABCD=S△ABD+S△BCD= ![]() ×6×2
×6×2 ![]() +
+ ![]() ×
× ![]() ×4=
×4= ![]() (m2)
(m2)
【解析】(1)求出第4个角度数,按照定义即可判断出结论;(2)利用等边对等角定理,须连接BD,得出有一组对角相等,再证另一组对角不等,得出结论;(3)借鉴(2)的方法,要使∠BCD=60°,C需在以BD为弦的弧BD上,若四边形ABCD的面积最大,则点C在边BE上,才能使高最大,进而面积最大.
【考点精析】掌握三角形的面积和圆周角定理是解答本题的根本,需要知道三角形的面积=1/2×底×高;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 .
.


(1)如图1,直接写出
 ,
, 和
和 之间的数量关系.
之间的数量关系.(2)如图2,
 ,
, 分别平分
分别平分 ,
, ,那么
,那么 和
和 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.(3)若点E的位置如图3所示,
 ,
, 仍分别平分
仍分别平分 ,
, ,请直接写出
,请直接写出 和
和 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】大于
 的正整数
的正整数 的三次幂可“裂变”成若干个连续奇数的和,如
的三次幂可“裂变”成若干个连续奇数的和,如 ,
, ,
, ,
, .若
.若 “裂变”后,其中有一个奇数是
“裂变”后,其中有一个奇数是 ,则
,则 的值是( )
的值是( )A.
 B.
B. C.
C.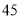 D.
D.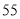
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:y=ax2+bx+4与x轴交于A(﹣3,0),B两点,与y轴交于点C,点M(﹣
 ,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了
 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等.
展开式中的系数等等.
(1)根据上面的规律,写出
 的展开式.
的展开式.(2)利用上面的规律计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某化工厂一期工程完成后购买了
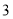 台甲型和
台甲型和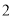 台乙型污水处理设备,共花费资金
台乙型污水处理设备,共花费资金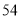 万元,且每台乙型设备的价格是每台甲型设备价格的
万元,且每台乙型设备的价格是每台甲型设备价格的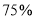 ,实际运行中发现,每台甲型设备每月能处理污水
,实际运行中发现,每台甲型设备每月能处理污水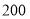 吨,每台乙型设备每月能处理污水
吨,每台乙型设备每月能处理污水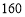 吨.今年该厂二期工程即将完成产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共
吨.今年该厂二期工程即将完成产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共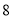 台用于二期工程的污水处理,预算本次购买资金不超过
台用于二期工程的污水处理,预算本次购买资金不超过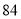 万元,预计二期工程完成后每月将产生不少于
万元,预计二期工程完成后每月将产生不少于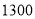 吨污水.
吨污水.(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元;
(2)请你求出用于二期工程的污水处理设备的所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,AD=8,点E在BC边上,且BE:EC=1:3.动点P从点B出发,沿BA运动到点A停止.过点E作EF⊥PE交边AD或CD于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为__________.

相关试题

