【题目】已知直线![]() .
.



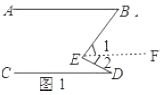
(1)如图1,直接写出![]() ,
,![]() 和
和![]() 之间的数量关系.
之间的数量关系.
(2)如图2,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
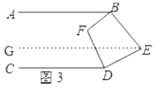
(3)若点E的位置如图3所示,![]() ,
,![]() 仍分别平分
仍分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系.
的数量关系.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)过点E作![]() ,根据平行线的性质得
,根据平行线的性质得![]() ,
,![]() ,进而即可得到结论;
,进而即可得到结论;
(2)由角平分线的定义得![]() ,
,![]() ,结合第(1)题的结论,即可求证;
,结合第(1)题的结论,即可求证;
(3)过点![]() 作
作![]() ,由平行线的性质得
,由平行线的性质得![]() ,结合第(1)题的结论与角平分线的定义得
,结合第(1)题的结论与角平分线的定义得![]() ,进而即可得到结论.
,进而即可得到结论.
(1)![]() ,理由如下:
,理由如下:
如图1,过点E作![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ;
;
(2)![]() .理由如下:
.理由如下:
∵![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由(1)得,![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)![]() ,理由如下:
,理由如下:
如图3,过点![]() 作
作![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由(1)知,![]() ,
,
又∵![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图把
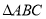 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到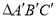 .
.(1)在图中画出
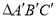 ;
;(2)写出点
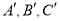 的坐标:
的坐标: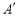 的坐标为______,
的坐标为______,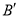 的坐标为 _________;
的坐标为 _________; 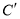 的坐标为________.
的坐标为________.(3)在
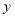 轴上是否存在一点P,使得
轴上是否存在一点P,使得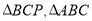 的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.
的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.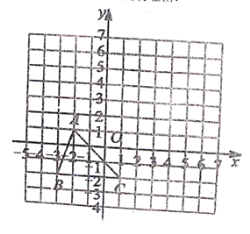
-
科目: 来源: 题型:
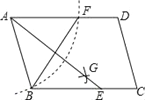
查看答案和解析>>【题目】如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,垂足分别为D,F,试说明:
,垂足分别为D,F,试说明: 请补充说明过程,并在括号内填上理由
请补充说明过程,并在括号内填上理由解:
 (已知)
(已知)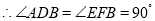 ( )
( ) ( )
( ) ( )
( ) (已知)
(已知) ( )
( ) ( )
( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于
 的正整数
的正整数 的三次幂可“裂变”成若干个连续奇数的和,如
的三次幂可“裂变”成若干个连续奇数的和,如 ,
, ,
, ,
, .若
.若 “裂变”后,其中有一个奇数是
“裂变”后,其中有一个奇数是 ,则
,则 的值是( )
的值是( )A.
 B.
B. C.
C.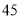 D.
D.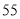
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:y=ax2+bx+4与x轴交于A(﹣3,0),B两点,与y轴交于点C,点M(﹣
 ,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)【探索体验】如图1,已知在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.求证:四边形ABCD是“等对角四边形”.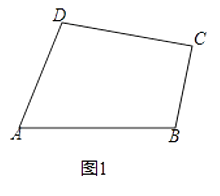
(2)如图2,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.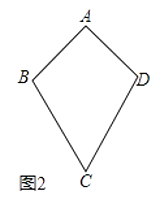
(3)【尝试应用】如图3,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4m,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.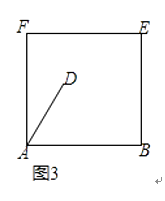
相关试题

