【题目】商店购进一种商品进行销售,进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将商品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月商品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?最大月利润时多少?
参考答案:
【答案】(1)y=![]()
(2)当销售价格为65元时,利润最大,最大利润为6250元.
【解析】试题分析:(1)根据题意售价每涨元每月要少卖件,售价每下降元每月要多卖件,根据等量关系列出方程即可;(2)根据每件商品的利润与商品销量的乘积即为总利润,列出与的函数关系式,再利用二次函数的性质可得到最大利润.
试题解析:
(1)y=![]()
(2)当0≤x≤30时
w=( 20+x )(( 300-10x )=-10x 2+100x+6000=-10( x-5 )2+6250
x=5时,w有最大值为6250
当-20≤x<0时
w=( 20+x )(( 300-20x )=-20x 2-100x+6000=-20( x+ ![]() )2+6125
)2+6125
x=-![]() 时,w有最大值为6125.
时,w有最大值为6125.
由题意知x应取整数,故当x=-2或x=-3时,w<6125<6250
所以,当销售价格为65元时,利润最大,最大利润为6250元.
-
科目: 来源: 题型:
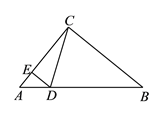
查看答案和解析>>【题目】如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E.设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P,问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=3x2向右平移一个单位,则所得抛物线的解析式为( )
A.y=3(x+1)2B.y=3(x-1)2C.y=3x2+1D.y=3x2-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3m)33n=( )
A.3mn
B.33m+n
C.27mn
D.27m+n -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BD为∠ABC的平分线.
(1)如图1,∠C=2∠DBC,∠A=60°,求证:△ABC为等边三角形;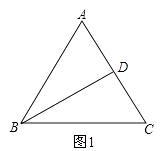
(2)如图2,若∠A=2∠C,BC=8,AB=4.8,求AD的长度;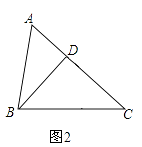
(3)如图3,若∠ABC=2∠ACB,∠ACB的平分线OC与BD相交于点O,且OC=AB,求∠A的度数.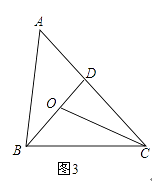
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
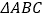 中,
中, .如图①,
.如图①,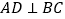 于点
于点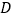 ,
,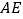 平分
平分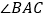 ,则易知
,则易知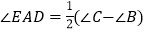 .
.(1)如图②,
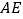 平分
平分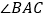 ,
, 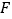 为
为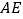 上的一点,且
上的一点,且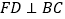 于点
于点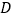 ,这时
,这时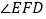 与
与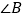 、
、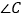 有何数量关系?请说明理由;
有何数量关系?请说明理由;(2)如图③,
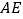 平分
平分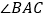 ,
,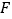 为
为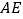 延长线上的一点,
延长线上的一点,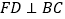 于点
于点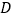 ,请你写出这时
,请你写出这时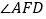 与
与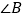 、
、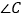 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).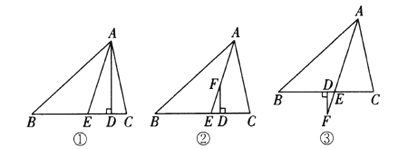
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是方程x2+ax+2=0的一个根,则a的值是( )
A.﹣2B.﹣3C.2D.3
相关试题

