搜索
【题目】用适当的方法解下列方程
（1）x2﹣4x+1＝0 （2）x2+5x+7＝0
（3）3x（x﹣1）＝2﹣2x （4）x2＝x+56
参考答案：
【答案】（1）2+
， 2﹣； （2）原方程无解； （3）1，﹣
； （4）8，﹣7．
【解析】
（1）移项后配方，开方，即可得出两个一元一次方程，求出方程的解即可；
（2）先求出b2-4ac的值，再判断即可；
（3）移项后分解因式，即可得出两个一元一次方程，求出方程的解即可；
（4）移项后分解因式，即可得出两个一元一次方程，求出方程的解即可．
（1）x2-4x+1=0，
x2-4x=-1，
x2-4x+4=-1+4，
（x-2）2=3，
x-2=±，
x1=2+，x2=2-；
（2）x2+5x+7=0，
b2-4ac=52-4×1×7=-3＜0，
所以原方程无解；
（3）3x（x-1）=2-2x，
3x（x-1）+2x-2=0，
3x（x-1）+2（x-1）=0，
（x-1）（3x+2）=0，
x-1=0，3x+2=0，
x1=1，x2=-；
（4）x2=x+56，
x2-x-56=0，
（x-8）（x+7）=0，
x-8=0，x+7=0，
x1=8，x2=-7．
-
科目： 来源： 题型：
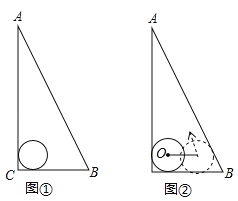
查看答案和解析>>【题目】如图，△ABC是一块直角三角板，且∠C=90°，∠A=30°，现将圆心为点O的圆形纸片放置在三角板内部．
（1）如图①，当圆形纸片与两直角边AC、BC都相切时，试用直尺与圆规作出射线CO；（不写作法与证明，保留作图痕迹）
（2）如图②，将圆形纸片沿着三角板的内部边缘滚动1周，回到起点位置时停止，若BC=9，圆形纸片的半径为2，求圆心O运动的路径长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,直线AB∥CD,点E在直线AB上,点G在直线CD上,点P在直线AB.CD之间,∠AEP=40°,∠EPG=900
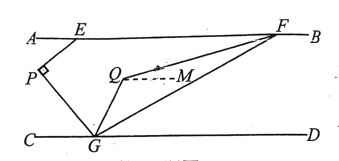
(1)填空:∠PGC=_________0；
(2)如图, 点F在直线AB上,联结FG,∠EFG的平分线与∠PGD的平分线相交于点Q，当点F在点E的右侧时,如果∠EFG=30°,求∠FQG的度数；
解:过点Q作QM∥CD
因为∠PGC+∠PGD=1800
由(1)得∠PGC=_______0,
所以∠PGD=1800-∠PGC=________0,
因为GQ平分∠PGD,
所以∠PGQ=∠QGD=
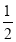∠PGD=_________0(下面请补充完整求∠FQG度数的解题过程)
(3)点F在直线AB上,联结FG,∠EFG的平分线与∠PGD的平分线相交于点Q.如果∠FQG=2∠BFG,请直接写出∠EFG的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班同学为了解2019年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行整理如下：
月均用水量x（t）
频数（户）
频率
6
0.12
0.24
16
0.32
10
0.20
4
2
0.04
请解答下列问题：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）求该小区用水量不超过15t的家庭占被调查家庭总数的百分比；
（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20t的家庭大约有多少户？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣（2k+1）x+k2+k＝0．
（1）求证：方程有两个不相等的实数根；
（2）若△ABC的两边AB，AC的长是这个方程的两个实数根．第三边BC的长为5，
①若△ABC是以BC为斜边的直角三角形，求k的值．
②若△ABC是等腰三角形，求k的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下.（单位：
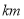）第一次
第二次
第三次
第四次
第五次
第六次
第七次
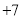
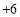
（1）求收工时，检修小组在
地的何方向？距离地多远？（2）在第几次纪录时距
地最远？（3）若汽车行驶每千米耗油0.4升，问从
地出发，检修结束后再回到地共耗油多少升？ -
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数分别填入相应的集合里
-4,
, 
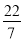, 0, -3.14, 717, -(+5) +1.88,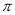 
(1)正有理数集合：{_____________________________…}
(2)负数集合：{_____________________________…}
(3)整数集合：{_____________________________ …}
(4)分数集合：{______________________________…}
相关试题
