【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
参考答案:
【答案】(1)在A地的东边,距离A地1km;(2)第三次记录;(3)16.8升;
【解析】
(1)把所有行驶记录相加,再根据正数和负数的意义解答;
(2)分别写出各次记录时距离A地的距离,然后判断即可;
(3)把所有行驶记录的绝对值相加,再乘以0.4计算即可得解.
(1)-4+7-9+8+6-5-2=1
答:在A地的东面1km处;
(2)第一次距A地|-4|=4千米;
第二次:|-4+7|=3千米;
第三次:|-4+7-9|=6千米;
第四次:|-4+7-9+8|=2千米;
第五次:|-4+7-9+8+6|=8千米;
第六次:|-4+7-9+8+6-5|=3千米;
第七次:|-4+7-9+8+6-5-2|=1千米
第5次记录是离A地最远
(3)从出发到收工汽车行驶的总路程:|-4|+|+7|+|-9|+|+8|+|+6|+|-5|+|-2|+|1|=42(km)从出发到收工共耗油:42×0.4=16.8(升).
答:从出发到收工共耗油16.8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
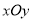 中,图形
中,图形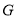 的投影矩形定义如下:矩形的两组对边分别平行于
的投影矩形定义如下:矩形的两组对边分别平行于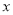 轴,
轴,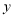 轴,图形
轴,图形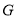 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为
的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为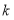 ,我们称常数
,我们称常数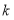 为图形
为图形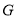 的投影比,如图1,矩形
的投影比,如图1,矩形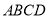 为
为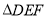 的投影矩形,其投影比
的投影矩形,其投影比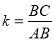 .
.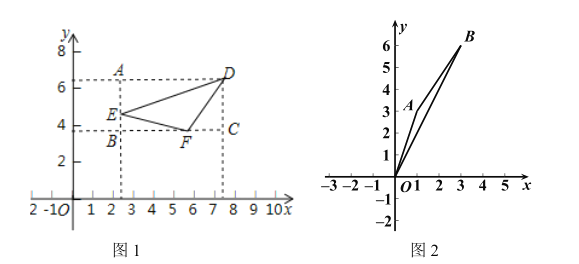
(1)如图2,若点
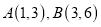 ,则
,则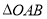 投影比
投影比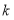 的值为________________;
的值为________________;(2)已知点
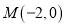 ,点
,点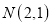 ,且
,且 投影比
投影比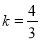 ,则
,则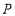 点坐标可能是__________(填写序号);
点坐标可能是__________(填写序号);①
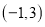 ②
② ③
③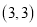 ④
④
(3)已知点
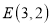 ,在直线
,在直线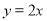 上有一点
上有一点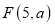 和一动点
和一动点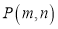 ,且
,且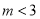 ,是否存在这样的
,是否存在这样的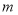 ,使得
,使得 的投影比
的投影比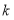 为定值?若存在,请求出
为定值?若存在,请求出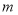 的范围及定值
的范围及定值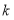 ;若不存在,请说明理由.
;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C在线段AB上,线段AC=10 cm,BC=4 cm,取线段AC、BC的中点D、E.

(1)请你计算线段DE的长是多少?
(2)观察DE的大小与线段AB的关系,你能用一句简洁的话将这种关系表述出来吗?
(3)若点C为直线AB上的一点,其他条件不变,线段DE的长会改变吗?如果改变,请你求出DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,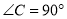 ,以
,以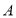 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交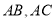 于点
于点 和
和 ,再分别以
,再分别以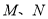 为圆心,大于
为圆心,大于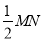 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点 ,连接
,连接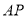 并延长交
并延长交 于点
于点 ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为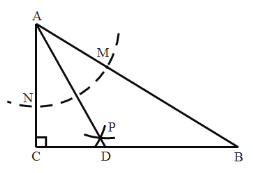
①
 是
是 的平分线;
的平分线;②若
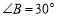 ,则
,则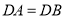 ;
;③
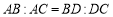 ;
;④点
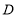 在
在 的垂直平分线上.
的垂直平分线上.A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是半径为3的⊙O上的点,
 尺规作图:作⊙O的内接正六边形ABCDEF;
尺规作图:作⊙O的内接正六边形ABCDEF;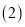 求
求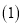 中弧AC的长.
中弧AC的长.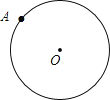
-
科目: 来源: 题型:
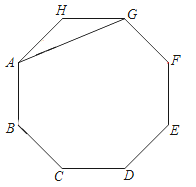
查看答案和解析>>【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕
 )的值;
)的值;(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
相关试题

