【题目】如图,在四边形AECF中,![]() .CE、CF分别是△ABC的内,外角平分线.
.CE、CF分别是△ABC的内,外角平分线.

(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
参考答案:
【答案】(1)见解析;(2)当![]() 满足
满足![]() 时,四边形AECF是正方形,见解析.
时,四边形AECF是正方形,见解析.
【解析】
(1)求出∠ECF=90°=∠E=∠F,即可推出答案;
(2)∠ACB=90°,推出∠ACE=∠EAC=45°,AE=CE即可.
(1)证明:∵CE、CF分别是![]() 的内、外角平分线,
的内、外角平分线,
![]() ,
,![]() .
.
![]() ,即
,即![]() .
.
![]() ,
,
∴四边形AECF是矩形.
(2)解:当![]() 满足
满足![]() 时,四边形AECF是正方形.
时,四边形AECF是正方形.
理由:![]()
![]()
![]() .
.![]() .
.
∵四边形AECF是矩形,∴四边形AECF是正方形.
故答案为:(1)见解析;(2)当![]() 满足
满足![]() 时,四边形AECF是正方形,见解析.
时,四边形AECF是正方形,见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
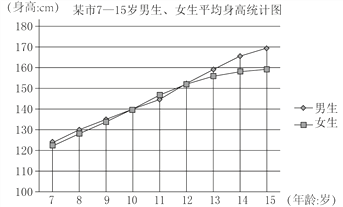
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
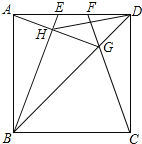
查看答案和解析>>【题目】如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级学生参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下(单位:分):
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分数段整理数据并补全表格:
成绩x
人数 年级




七年级
1
1
5
3
八年级
4
4
分析数据:补全下列表格中的统计量:
统计量
年级
平均数
中位数
众数
方差
七年级
93.6
94
24.2
八年级
93.7
93
20.4
得出结论:你认为哪个年级学生“汉字听写”大赛的成绩比较好?并说明理由.(至少从两个不同的角度说明推断的合理性)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
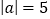 |,
|,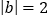 ,且
,且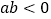 ,求
,求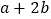 的值.
的值.解:(1)因为
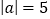 ,所以
,所以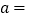 ______;
______;因为
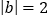 ,所以
,所以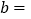 ______;
______;又因为
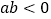 ,
,所以当
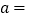 ______时,
______时,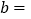 ______;
______;或当
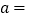 ______时,
______时,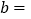 ______,
______,∴
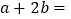 ______或_______.
______或_______.
相关试题

