搜索
【题目】已知
|，
，且
，求
的值．
解：（1）因为，所以
______；
因为，所以
______；
又因为，
所以当______时，______；
或当______时，______，
∴
______或_______．
参考答案：
【答案】±5, ±2,5,-2,-5,2,1,-1
【解析】
根据绝对值的定义数轴上对应的点与原点的距离叫做该数绝对值，得出a，b的值，再根据ab＜0，可知a，b一正一负，求出所要求的值.
解：（1）∵数轴上对应的点与原点的距离叫做该数绝对值，|a|=5，|b|=2，
∴a=±5，b=±2，
∵ab＜0，
∴a，b一正一负，
得出a=5，b=-2或a=-5，b=2，
∴
5+2×（-2）=1或（-5）+2×2=-1，
故答案为±5，±2，5，-2，-5，2，1，-1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一位射击运动员在10次射击训练中，命中靶的环数如图． 请你根据图表，完成下列问题：
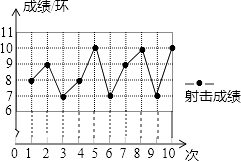
（1）补充完成下面成绩表单的填写：射击序次
1
2
3
4
5
6
7
8
9
10
成绩/环
8
10
7
9
10
7
10
（2）求该运动员这10次射击训练的平均成绩． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t(秒).
(1)当t为何值时，四边形PQDC是平行四边形
(2)当t为何值时，以C,D,Q,P为顶点的梯形面积等于60cm2？
(3)是否存在点P，使△PQD是等腰三角形？若存在，请求出所有满足要求的t的值，若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，BD⊥AC，AB=6，AC=5
，∠A=30°．
①求BD和AD的长；
②求tanC的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有4张写着以下数字的卡片，请按要求抽出卡片，完成下列各题：
（1）从中取出2张卡片，使这2张卡片上数字之积最大，最大值是________．
（2）从中取出2张卡片，使这2张卡片上数字之差最小，最小值是________．
（3）从中取出4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，请写出一种符合要求的运算式子________．（注：4个数字都必须用到且只能用一次.）
-
科目： 来源： 题型：
查看答案和解析>>【题目】数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．在数轴上若点A、B分别表示有理数a、b ，在数轴上A、B两点之间的距离AB=| a-b | ．结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示﹣3和2的两点之间的距离是_____；数轴上表示 x 和 -3 两点之间的距离是_____；
（2）若a表示一个有理数，则|a+4|+|a﹣2|有最小值吗？若有，请求出最小值；若没有，请说明理由；
（3）当a =_____时，|a+4|+|a﹣1|+|a﹣2|的值最小，最小值是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上点A表示的有理数为﹣6，点B表示的有理数为6，点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动，当点P到达点B后立即返回，仍然以每秒4个单位长度的速度运动至点A停止运动，设运动时间为t（单位：秒）．
（1）求t＝1时点P表示的有理数；
（2）求点P与点B重合时的t值；
（3）在点P沿数轴由点A到点B再回到点A的运动过程中，求点P与点A的距离（用含t的代数式表示）；
（4）当点P表示的有理数与原点的距离是2个单位长度时，请求出所有满足条件的t值．
相关试题
