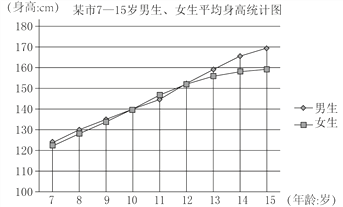
【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
A. ①③ B. ②③ C. ②④ D. ③④
参考答案:
【答案】C
【解析】分析:对所给的折线图进行分析,得出相关信息并对四个结论一一判断即可得出答案.
详解:由折线图可知,10岁之前,同龄的男生的平均身高一般会略高于女生的平均身高,故①错误;
10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生,故②正确;
7~15岁期间,男生的平均身高先高于女生的平均身高再略低于女生的平均身高最后高于女生的平均身高,故③错误;
13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大,故④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数式书写规范的是( )
A. a÷3B. a8C. 5aD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点
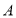 、
、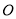 、
、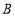 依次在直线
依次在直线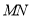 上,现将射线
上,现将射线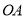 绕点
绕点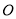 沿顺时针方向以每秒
沿顺时针方向以每秒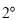 的速度旋转,同时射线
的速度旋转,同时射线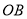 绕点
绕点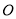 沿逆时针方向以每秒
沿逆时针方向以每秒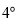 的速度旋转,如图
的速度旋转,如图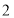 ,设旋转时间为
,设旋转时间为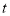 (
(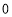 秒
秒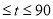 秒).
秒).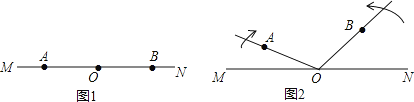
(1)用含
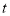 的代数式表示
的代数式表示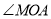 的度数.
的度数.(2)在运动过程中,当
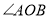 第二次达到
第二次达到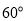 时,求
时,求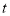 的值.
的值.(3)在旋转过程中是否存在这样的
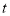 ,使得射线
,使得射线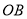 是由射线
是由射线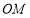 、射线
、射线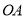 、射线
、射线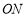 中的其中两条组成的角(指大于
中的其中两条组成的角(指大于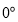 而不超过
而不超过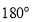 的角)的平分线?如果存在,请直接写出
的角)的平分线?如果存在,请直接写出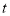 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OM上有三点A、B、C,OC=45cm, BC=15cm, AB=30cm,已知动点P、Q同时运动,其中动点P从点O出发沿OM方向以速度2cm/s匀速运动,动点Q从点C出发沿CA方向匀速运动,当点Q运动到点A时,点Q停止运动(点P继续运动).设运动时间为t秒.

(1)求点P运动到点B所用的时间;
(2)若点Q运动速度为每秒1cm,经过多少秒时,点P和点Q的距离为30cm;
(3)当PA=2PB时,点Q恰好在线段AB的三等分点的位置,求点Q的速度.
-
科目: 来源: 题型:
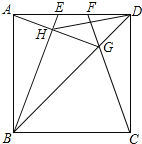
查看答案和解析>>【题目】如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形AECF中,
 .CE、CF分别是△ABC的内,外角平分线.
.CE、CF分别是△ABC的内,外角平分线.
(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
相关试题

