【题目】如图:三角形ABC内接于圆O,∠BAC与∠ABC的角平分线AE,BE相交于点E,延长AE交外接圆O于点D,连接BD,DC,且∠BCA=60°
(1)求∠BED的大小;
(2)证明:△BED为等边三角形;
(3)若∠ADC=30°,圆O的半径为r,求等边三角形BED的边长.
参考答案:
【答案】
(1)解:∵∠BCA=60°,
∴∠BAC+∠ABC=180°-∠BCA=180°-60°=120°,
∵∠BAC与∠ABC的角平分线AE,BE相交于点E,
∴∠ABE+∠BAE= ![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)= ![]() ×120°=60°,
×120°=60°,
∴∠BED=∠ABE+∠BAE=60°
(2)证明:∵∠BCA=60°,
∴∠ADB=∠BCA=60°,
∴∠DBE=180°-∠BED-∠ADB=180°-60°-60°=60°,
∴△BED为等边三角形
(3)解:∵∠ADC=30°,∠ADB=60°,
∴∠BDC=∠ADC+∠ADB=30°+60°=90°,
∴BC是⊙O的直径,
∵∠BCA=60°,
∴∠ABC=90°-60°=30°,
∵BE平分∠ABC,
∴∠CBE=15°,
∴∠DBC=∠DBE-∠CBE=60°-15°=45°,
∴BD=BCcos45°=2r× ![]() =
= ![]() r.
r.
即等边△BED的边长为 ![]() r
r
【解析】(1)根据三角形内角和定理和三角形的一个外角等于和它不相邻的两个内角的和,求出∠BED的值;(2)根据圆周角定理和三角形内角和定理得到△BED为等边三角形;(3)根据圆周角定理,得到BC是⊙O的直径,根据角平分线定义求出∠CBE的度数,根据三角函数求出等边△BED的边长.
【考点精析】掌握圆周角定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
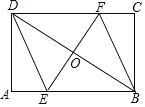
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t >0)秒.
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒1个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问点P运动多少秒时P、Q两点相遇?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出相应图形,并求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请比较哪种方案的最大利润更高,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
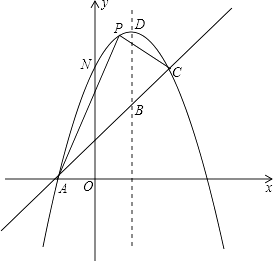
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:
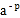 =
= (a≠0),即a的负P次幂等于a的p次幂的倒数.例:
(a≠0),即a的负P次幂等于a的p次幂的倒数.例: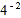 =
=
(1)计算:
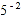 =__;
=__; =__;
=__;(2)如果
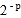 =
= ,那么p=__;如果
,那么p=__;如果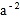 =
=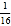 ,那么a=__;
,那么a=__;(3)如果
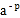 =
= ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )

A. 点F B. 点E C. 点A D. 点C
相关试题

