Question

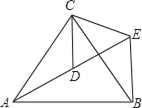
【题目】已知点O是等腰直角三角形ABC斜边上的中点，AB=BC,E是AC上一点，连结EB.

(1) 如图1，若点E在线段AC上,过点A作AM⊥BE，垂足为M，交BO于点F．求证：OE=OF；

(2)如图2，若点E在AC的延长线上，AM⊥BE于点M，交OB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由.

Answer 1

【答案】见解析

【解析】试题分析：（1）由三角形ABC是等腰直角三角形，AB=BC，得到∠BAC=∠ACB=45°，又由点O是AC边上的中点，得到∠BOE=∠AOF=90°，∠ABO=∠CBO=45°，从而得到∠BAC=∠ABO，OB=OA，又由AM⊥BE，得到∠MEA+∠MAE=90°=∠AFO+∠MAE，

故有∠MEA=∠AFO，得到Rt△BOE≌Rt△AOF，从而得到结论；

（2）同（1）可证明Rt△BOE≌Rt△AOF，从而得到OE=OF．

试题解析：（1）证明：∵三角形ABC是等腰直角三角形，AB=BC，

∴∠BAC=∠ACB=45°

又点O是AC边上的中点，

∴∠BOE=∠AOF=90°，∠ABO=∠CBO=45°

∴∠BAC=∠ABO，∴OB=OA，

又∵AM⊥BE，

∴∠MEA+∠MAE=90°=∠AFO+∠MAE，

∴∠MEA=∠AFO，

∴Rt△BOE≌Rt△AOF，∴OE=OF；

（2）OE=OF成立；

证明：∵三角形ABC是等腰直角三角形，AB=BC，

∴∠BAC=∠ACB=45°

又点O是AC边上的中点，

∴∠BOE=∠AOF=90°，∠ABO=∠CBO=45°

∴∠BAC=∠ABO，∴OB=OA，

又∵AM⊥BE，

∴∠F+∠MBF=90°=∠B+∠OBE，

又∵∠MBF=∠OBE，∴∠F=∠E，

∴Rt△BOE≌Rt△AOF，

∴OE=OF．