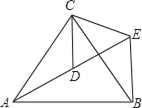
【题目】如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:AD=BE;
(2)求∠AEB的度数.
参考答案:
【答案】(1)证明见解析;(2)∠AEB=60°.
【解析】(1)根据等边三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,求出∠ACD=∠BCE,然后根据SAS证明△ACD≌△BCE,即可得出AD=BE;
(2)由△ECD是等边三角形可得∠CDE=∠CED=60°,根据补角的性质可求∠ADC=120°,根据全等三角形的性质可得∠BEC=∠ADC=120°,进而根据∠AEB=∠BEC﹣∠CED可得出答案.
证明:(1)∵△ACB和△ECD都是等边三角形,
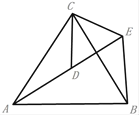
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
又∵∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
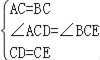
∴△ACD≌△BCE(SAS).
∴AD=BE;
(2)在等边△ECD中,
∠CDE=∠CED=60°,
∴∠ADC=120°,
∵△ACD≌△BCE,
∴∠BEC=∠ADC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )

A. 3 B. 2 C.
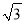 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(3m﹣5n+4mn)﹣2(m﹣2n+3mn),其中m﹣n=7,mn=﹣5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点C(-4,0),点
 分别在
分别在 轴,
轴,  轴的正半轴上,线段OA、OB的长度都是方程
轴的正半轴上,线段OA、OB的长度都是方程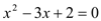 .的解,且OB>OA。若点
.的解,且OB>OA。若点 从
从 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线 运动,连结
运动,连结 。
。(1)判断三角形ABC的形状
(2)求出
 的面积
的面积 关于点
关于点 的运动时间
的运动时间 秒的函数关系式.
秒的函数关系式.(3)在点P的运动过程中,利用备用图探究,求
 周长最短时点P运动的时间。
周长最短时点P运动的时间。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A.1:2
B.1:4
C.1:5
D.1:16 -
科目: 来源: 题型:
查看答案和解析>>【题目】“比a大1的数”用代数式表示是 ( )
A. a+1B. -a+1C. aD. a-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求对0.05049分别取近似值,其中错误的是( )
A.0.1(精确到十分位)
B.0.05(精确到百分位)
C.0.05(精确到千分位)
D.0.050(精确到0.001)
相关试题

