【题目】如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,

(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
∠α的度数 | ______° | _____° | ______° | ______° | …… | _____° |
(2)根据规律,计算正八边形中的∠α的度数.
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
参考答案:
【答案】(1)60,45,36,30°,![]() ;(2)22.5;(3)不存在.
;(2)22.5;(3)不存在.
【解析】
(1)根据计算、观察,可发现规律:正n边形中的∠α=(![]() )°;
)°;
(2)根据规律,可得正八边形中的∠α的度数;
(3)根据正n边形中的∠α=(![]() )°,可得答案.
)°,可得答案.
(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° | 36° | 30° | … | ( |
(2)根据规律,计算正八边形中的∠α=(![]() )°=22.5°;
)°=22.5°;
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=(![]() )°.
)°.
解得n=8![]() ,n是正整数,n=8
,n是正整数,n=8![]() (不符合题意要舍去),
(不符合题意要舍去),
不存在正n边形使得∠α=21°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(m,0),点B的坐标为(m﹣2,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,C′关于直线x=m对称,BC′交直线x=m于点E,若△BOE的面积为4,则点E的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据图1,图2所提供的信息,解答下列问题:
(1)2007年海南省城镇居民人均可支配收入为 元,比2006年增长 %;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年 (填“增加”或“减少”).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据
 ≈1.41,
≈1.41,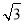 ≈1.73.
≈1.73.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
 地出发,匀速驶向
地出发,匀速驶向 地.甲车以
地.甲车以 的速度行驶
的速度行驶 后,乙车才沿相同路线行驶.乙车先到达
后,乙车才沿相同路线行驶.乙车先到达 地并停留
地并停留 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离 与乙车行驶时间
与乙车行驶时间 之间的函数关系如图所示.下列说法:①乙车的速度是
之间的函数关系如图所示.下列说法:①乙车的速度是 ;②
;② ;③点
;③点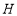 的坐标是
的坐标是 ;④
;④ .其中说法正确的是_________.
.其中说法正确的是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD·OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2,
 .
.①求⊙O的半径;②求sin∠BAD的值

相关试题

