【题目】阅读材料:
若a,b都是非负实数,则a+b≥2![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明: ∵(![]() -
-![]() )2≥0,∴a-2
)2≥0,∴a-2![]() +b≥0.
+b≥0.
∴a+b≥2![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:
已知x>0,求函数y=2x+![]() 的最小值.
的最小值.
解:y=2x+![]() ≥2
≥2![]() =4.当且仅当2x=
=4.当且仅当2x=![]() ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:
汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶(含70公里和110公里),每公里耗油(![]() +
+![]() )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
参考答案:
【答案】(1)y=![]() +
+![]() (70≤x≤110)(2)11.1升.
(70≤x≤110)(2)11.1升.
【解析】试题分析: ![]() 根据耗油总量=每公里的耗油量×行驶的速度,列出函数关系式即可.
根据耗油总量=每公里的耗油量×行驶的速度,列出函数关系式即可.![]() 经济时速就是耗油量最小时的速度.
经济时速就是耗油量最小时的速度.
试题解析: ![]() ∵汽车在每小时
∵汽车在每小时![]() 公里之间行驶时(含
公里之间行驶时(含![]() 公里和
公里和![]() 公里),每公里耗油
公里),每公里耗油![]() 升.
升.
![]()
![]() 根据材料得:
根据材料得: ![]() 时
时![]() 有最小值,
有最小值,
解得: ![]()
∴该汽车的经济时速为![]() 千米/小时.
千米/小时.
当![]() 时百公里耗油量为
时百公里耗油量为![]() 升.
升.
答: ![]()
![]() 关于
关于![]() 的函数关系式为:
的函数关系式为: ![]()
![]() 该汽车的经济时速为
该汽车的经济时速为![]() 千米/小时,经济时速的百公里耗油量为
千米/小时,经济时速的百公里耗油量为![]() 升.
升.
-
科目: 来源: 题型:
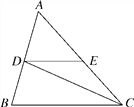
查看答案和解析>>【题目】如图,已知CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.求:
(1)∠EDC的度数;
(2)∠B的度数.
-
科目: 来源: 题型:
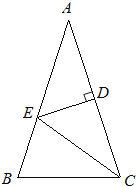
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求
ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求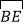 的度数和
的度数和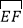 的度数.
的度数.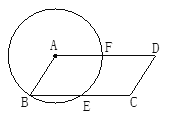
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=0.32,b=﹣3﹣2,c=
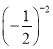 ,d=
,d=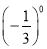 ,则它们的大小关系是( )
,则它们的大小关系是( )A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
-
科目: 来源: 题型:
查看答案和解析>>【题目】为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋顶收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如下表:
小明家
爷爷家
屋顶收集雨水的面积/m2
160
120
蓄水池的容积/ m3
50
13
蓄水池已有水的量/ m3
34
11.5
气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的
水注入小明家的蓄水池?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

相关试题

