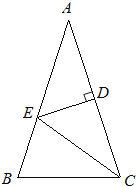
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
参考答案:
【答案】(1)36°;(2)5
【解析】试题分析:
(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°,又∠BEC=∠A+∠ECA=72°,所以BC=EC=5.
试题解析:
解:(1)∵DE垂直平分AC,∠A=36°∴CE=AE,∴∠ECD=∠A=36°;(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,∴∠BEC=∠A+∠ECD=72°,∴∠BEC=∠B,∴BC=EC=5.
(2)∵AB=AC,∠A=36°,∴∠B=(180°-36°)÷2=72°.
∵∠BEC=∠A+∠ECA=72°,∴CE=CB,∴BC=EC=5.
-
科目: 来源: 题型:
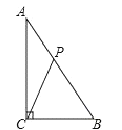
查看答案和解析>>【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
A. 5 B. 5或8 C.
 D. 4或
D. 4或
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
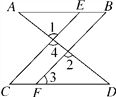
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
-
科目: 来源: 题型:
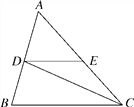
查看答案和解析>>【题目】如图,已知CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.求:
(1)∠EDC的度数;
(2)∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求
ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求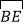 的度数和
的度数和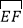 的度数.
的度数.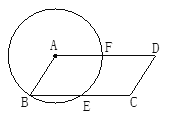
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
若a,b都是非负实数,则a+b≥2
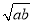 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.证明: ∵(
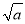 -
-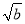 )2≥0,∴a-2
)2≥0,∴a-2 +b≥0.
+b≥0.∴a+b≥2
 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.举例应用:
已知x>0,求函数y=2x+
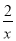 的最小值.
的最小值.解:y=2x+
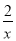 ≥2
≥2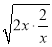 =4.当且仅当2x=
=4.当且仅当2x= ,即x=1时,“=”成立.
,即x=1时,“=”成立.当x=1时,函数取得最小值,y最小=4.
问题解决:
汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶(含70公里和110公里),每公里耗油(
 +
+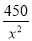 )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=0.32,b=﹣3﹣2,c=
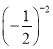 ,d=
,d=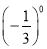 ,则它们的大小关系是( )
,则它们的大小关系是( )A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
相关试题

