搜索
【题目】如图，以
的边
、
为边的等边三角
和等边三角形
，四边形
是平行四边形．
当
满足什么条件时，四边形是矩形；
当满足什么条件时，平行四边形不存在；
当分别满足什么条件时，平行四边形是菱形，正方形？
参考答案：
【答案】
当
时，四边形
是矩形； 
当
时平行四边形不存在，当
、时平行四边形是正方形．
【解析】
（1）根据矩形的四角相等为90度求解；
（2）根据D、A、E在同一条直线上时不能构成四边形求解；
（3）分别根据菱形的四边相等和正方形的四边相等，四角相等的特性解题．
当时，四边形是矩形，
∴
；
∵四边形是平行四边形，
∴四边形是矩形（有一个角是直角的平行四边形是矩形）；
当时平行四边形不存在，
；
当且
不等于
时平行四边形是菱形．
综上可知：当、时平行四边形是正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=﹣
x+6分别交x轴、y轴于A、B两点，抛物线y=﹣ 
x2+8，与y轴交于点D，点P是抛物线在第一象限部分上的一动点，过点P作PC⊥x轴于点C．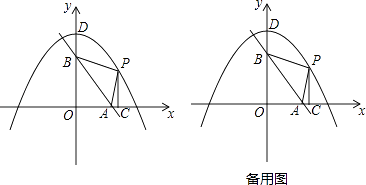
（1）点A的坐标为 ， 点D的坐标为；
（2）探究发现：
①假设P与点D重合，则PB+PC=；（直接填写答案）
②试判断：对于任意一点P，PB+PC的值是否为定值？并说明理由；
（3）试判断△PAB的面积是否存在最大值？若存在，求出最大值，并求出此时点P的坐标；若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，三角形ABC的顶点坐标分别为
，
，
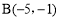，把三角形ABC向右平移2个单位长度，再向下平移4个单位长度后得到三角形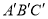
． （1）画出三角形ABC和平移后
的图形；（2）写出三个顶点
，
，
的坐标；（3）求三角形ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知A、B两地相距40千米，中午12：00时，甲从A地出发开车到B地，12：10时乙从B地出发骑自行车到A地，设甲行驶的时间为t（分），甲、乙两人离A地的距离S（千米）与时间t（分）之间的关系如图所示．由图中的信息可知，乙到达A地的时间为（ ）
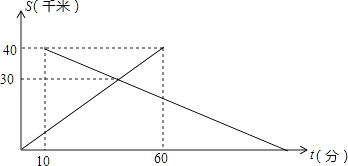
A.14：00
B.14：20
C.14：30
D.14：40 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=x2+bx+c与坐标轴交于A，B两点，则一元二次方程x2+bx+c=0的根的情况是( )
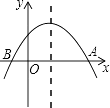
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.可能有实数根，也可能没有实数根 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起，∠DEA＝∠ACB＝90°，∠DAE＝∠ABC＝30°，E、A、C三点在一条直线上，连接BD，取BD中点M，连接ME、MC，试判断△EMC的形状，并说明理由．
-
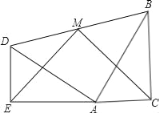
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，AC与BD相交于0，AE⊥BD于E，CF⊥BD于F，则图中的全等三角形共（ ）
A. 5对B. 6对C. 7对D. 8对
相关试题
