【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)OA可能在∠BOD的内部,也可能在∠BOD的外部,请分两种情况,在下图中用直尺、量角器画出射线OD,ON的准确位置;
(2)当α=40°时,求(1)中∠MON的度数,要求写出计算过程;
(3)用含α的代数式表示∠MON的度数.(直接写出结果即可)

参考答案:
【答案】(1)详见解析;(2)∠MON=135°或5°;(3)∠MON=135°或45°﹣α.
【解析】
(1)分射线OA在∠BOD的外部和内部两种情况作出图形;
(2)根据互为余角和补角的定义求出∠AOC和∠BOD的度数,再根据角平分线的定义可得∠MOA=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB﹣∠MOA﹣∠AOB分别代入数据进行计算即可得解;
∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB﹣∠MOA﹣∠AOB分别代入数据进行计算即可得解;
(3)分射线OA在∠BOD的外部和内部两种情况解答.
(1)如图1,图2所示;
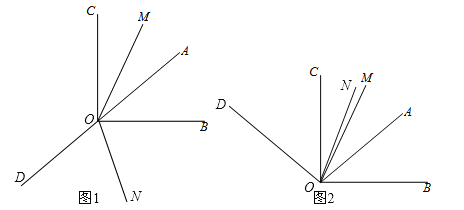
(2)∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,∴∠AOC=90°﹣∠AOB=50°,∠BOD=180°﹣∠AOB=140°.
∵OM平分∠AOC,ON平分∠BOD,∴∠MOA=![]() ∠AOC=
∠AOC=![]() ×50°=25°,∠BON=
×50°=25°,∠BON=![]() ∠BOD=
∠BOD=![]() ×140°=70°.
×140°=70°.
①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°;
②如图2,∠MON=∠NOB﹣∠MOA﹣∠AOB=70°﹣25°﹣40°=5°;
∴∠MON=135°或5°;
(3)∠MON=135°或45°﹣α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2
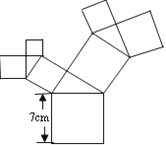
A. 28 B. 49 C. 98 D. 147
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
时间x(天)
0
4
8
12
16
20
销量y1(万朵)
0
16
24
24
16
0
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.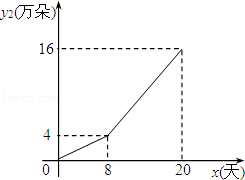
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )

A. 2B.
 C. 4D.
C. 4D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=
 x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=  x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
相关试题

