【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y= ![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= ![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒 ![]() 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
参考答案:
【答案】
(1)
解:∵矩形ABCO,B点坐标为(4,3)
∴C点坐标为(0,3)
∵抛物线y= ![]() x2+bx+c经过矩形ABCO的顶点B、C,
x2+bx+c经过矩形ABCO的顶点B、C,
∴ ![]() ,
,
解得: ![]() ,
,
∴该抛物线解析式y=﹣ ![]() x2+2x+3,
x2+2x+3,
设直线AD的解析式为y=k1x+b1
∵A(4,0)、D(2,3),
∴ ![]() ∴
∴  ,
,
∴ ![]() ,
,
联立 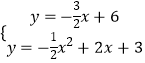 ,
,
∵F点在第四象限,
∴F(6,﹣3);
(2)
解:①∵E(0,6),∴CE=CO,(如图(1)),

连接CF交x轴于H′,过H′作BC的垂线交BC于P′,当P
运动到P′,当H运动到H′时,EP+PH+HF的值最小.
设直线CF的解析式为y=k2x+b2
∵C(0,3)、F(6,﹣3),
∴ ![]() ,
,
解得: ![]() ,
,
∴y=﹣x+3
当y=0时,x=3,
∴H′(3,0),
∴CP=3,∴t=3;
②如图1过M作MN⊥OA交OA于N,
∵△AMN∽△AEO,
∴ ![]() ,
,
∴ ![]() ,
,
∴AN=t,MN= ![]() ,
,
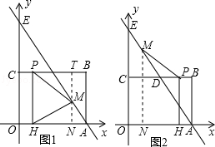
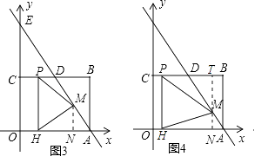
I如图3,当PM=HM时,M在PH的垂直平分线上,
∴MN= ![]() PH,
PH,
∴MN= ![]() ,
,
∴t=1;
II如图1,当HM=HP时,MH=3,MN= ![]() ,
,
HN=OA﹣AN﹣OH=4﹣2t 在Rt△HMN中,MN2+HN2=MH2,
∴ ![]() ,
,
即25t2﹣64t+28=0,
解得:t1=2(舍去), ![]() ;
;
III如图2,图4,当PH=PM时,
∵PM=3,MT= ![]() ,PT=BC﹣CP﹣BT=|4﹣2t|,
,PT=BC﹣CP﹣BT=|4﹣2t|,
∴在Rt△PMT中,MT2+PT2=PM2,
即 ![]() ,
,
∴25t2﹣100t+64=0,
解得: ![]() ,
, ![]()
综上所述: ![]() ,
, ![]() ,1,
,1, ![]() .
.
【解析】(1)由矩形的性质可求出C点的坐标,把B和C点的坐标代入y= ![]() x2+bx+c求出b和c的值即可该抛物线解析式;设直线AD的解析式为y=k1x+b1把A(4,0)、D(2,3)代入求出一次函数的解析式,再联立二次函数和一次函数的解析式即可求出F点的坐标;(2)①连接CF交x轴于H′,过H′作BC的垂线交BC于P′,当P运动到P′,当H运动到H′时,EP+PH+HF的值最小;②过M作MN⊥OA交OA于N,再分别讨论当PM=HM时,M在PH的垂直平分线上,当PH=PM时,求出符合题意的t值即可.
x2+bx+c求出b和c的值即可该抛物线解析式;设直线AD的解析式为y=k1x+b1把A(4,0)、D(2,3)代入求出一次函数的解析式,再联立二次函数和一次函数的解析式即可求出F点的坐标;(2)①连接CF交x轴于H′,过H′作BC的垂线交BC于P′,当P运动到P′,当H运动到H′时,EP+PH+HF的值最小;②过M作MN⊥OA交OA于N,再分别讨论当PM=HM时,M在PH的垂直平分线上,当PH=PM时,求出符合题意的t值即可.
【考点精析】通过灵活运用相似三角形的性质,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)OA可能在∠BOD的内部,也可能在∠BOD的外部,请分两种情况,在下图中用直尺、量角器画出射线OD,ON的准确位置;
(2)当α=40°时,求(1)中∠MON的度数,要求写出计算过程;
(3)用含α的代数式表示∠MON的度数.(直接写出结果即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )

A. 2B.
 C. 4D.
C. 4D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
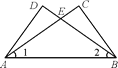
A. ∠DAE=∠CBE B. CE=DE C. △DAE与△CBE不一定全等 D. ∠1=∠2
-
科目: 来源: 题型:
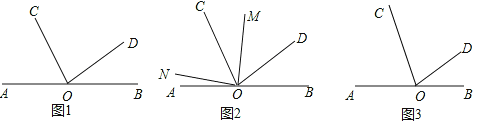
查看答案和解析>>【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=
 ∠AOC.
∠AOC.(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a与b满足
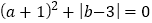 ,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为
,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为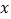 .
.(1)求a,b的值.
(2)若点 P 到点 A、点 B 的距离相等,求点P对应的数.
(3)现在点 A、点 B 分别以 2 个单位长度/秒和 0.5 个单位长度/秒的速度同时向右运动,点 P 以 3 个单位长度/秒的速度同时从原点向左运动.当点 A 与点 B 之间的距离为2个单位长度时,求点 P 所对应的数是多少?

相关试题

